Exponential formulas are at the heart of mathematics, science, and technology. Whether you’re calculating compound interest, modeling population growth, or understanding scientific notation, you’ll frequently encounter base and power in exponential formulas. These two components—base and power—form the foundation of exponential expressions.
In this guide, we’ll explore what base and power mean, how they work together, common mistakes to avoid, and how they appear in real-world applications. Whether you’re a student, teacher, or curious learner, this deep dive will help you grasp exponent concepts clearly and confidently.
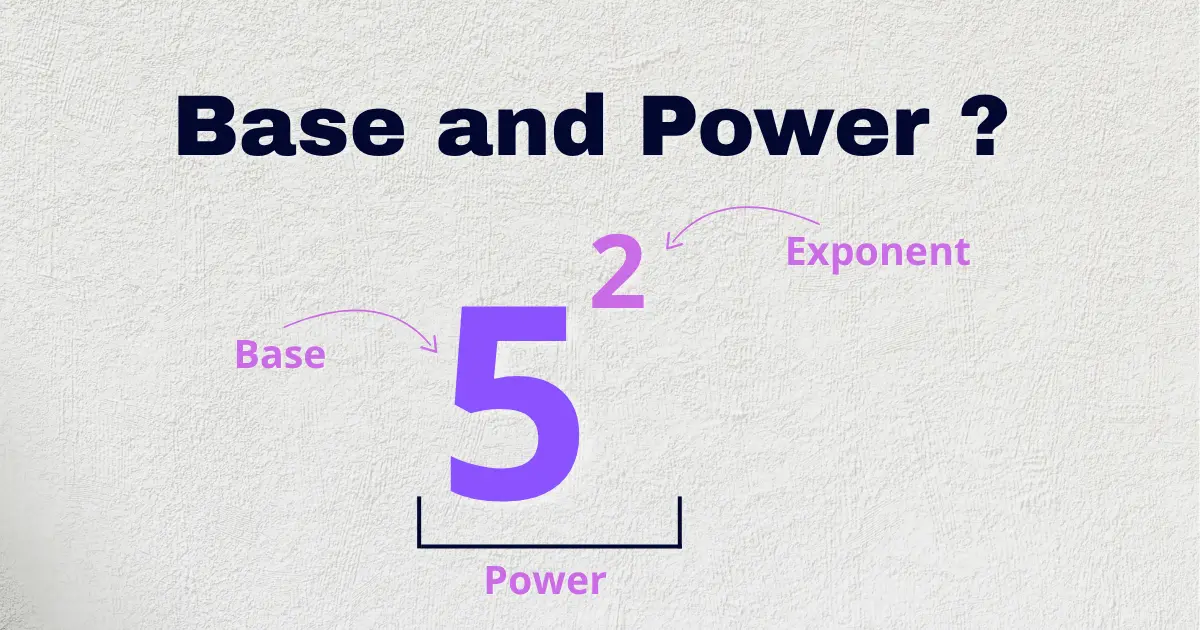
What Is a Base in an Exponential Expression?
In any exponential formula, the base is the number that gets multiplied repeatedly. It’s the starting point—the foundation on which powers act. In the expression $$232^{323}$$, the number 2 is the base. It tells us what number to multiply.
Understanding the base in exponent form is crucial because it determines the scale of the result. A base of 10 grows faster than a base of 2 when raised to the same power.
Examples of Common Bases
Some commonly used bases include:
- Base 2: Used in computing and binary systems.
- Base 10: The standard in everyday arithmetic and scientific notation.
- Base e (~2.718): Essential in calculus and natural exponential growth.
These examples of base numbers appear in everything from financial modeling to programming.
Visualizing the Base
To help visualize how a base works, imagine a number tree: start with the base at the root and multiply it by itself as many times as the exponent says. For example, $$81 = 3 \times 3 \times 3 \times 3 = 3^4 = 81$$
Base visuals and exponent diagrams are powerful learning tools. They show how the base repeats itself through multiplication, helping learners better understand the logic behind exponential formulas.
Why the Base Matters
Even a small change in the base can cause a significant shift in results. For instance:
$$25 = 3^{2} \times 2^{5}$$
$$35 = 24 \times 3 \times 3^5 = 24335 = 243$$
This illustrates the importance of base value in exponential growth. Understanding the role of the base helps you predict outcomes and model real-world phenomena more accurately.
What Does the Power Represent?
If the base is the foundation, the power (or exponent) is the instruction—it tells us how many times to multiply the base by itself. In $$535^{353}$$, the power is 3, which means multiply 5 three times:$$5 \times 5 \times 5 = 125$$
The power in exponential formulas controls the intensity of the multiplication. Larger powers lead to faster growth, and understanding this dynamic is crucial when solving exponent problems.
Positive Powers
Positive powers are the most common. They represent straightforward multiplication:
$$8^3 = 8 \times 8 \times 8 = 512$$
$$16^2 = 16 \times 16 = 256$$
$$10^5 = 100,000$$
These are clear examples of positive powers in action. They also show how quickly numbers grow when raised to higher powers.
Zero and One as Powers
Special exponent rules come into play with zero and one:
- Anything raised to the power of 1 stays the same: $$7^1 = 7$$
- Anything to the power of 0 equals 1: $$990=199^0 = 1$$
These exponent rules for 0 and 1 are critical to remember. They’re consistent across all math levels and serve as shortcuts in calculations.
Negative Powers
What does a negative exponent mean? A negative power indicates a reciprocal:
$$2^{-3} = \frac{1}{2^{3}} = \frac{1}{8}$$
This rule shows that negative exponents flip the base. Negative power examples appear frequently in algebra and scientific formulas.
Relationship Between Base and Power
The interaction between base and power determines the result of an exponential expression. Think of it as a team effort—while the base sets the number, the power decides the magnitude.
For example:
$$24 = 16 \times 2 \times 4$$
$$4^{2} = 16$$
Both result in the same value but are structurally different. The base-power relationship plays a key role in algebra, physics, and computer science.
Differences Between Exponential, Radical, and Linear Terms
Exponential formulas differ from other expressions in how they grow:
- Exponential: Involves multiplication and rapid growth (e.g., $$2n \times 2^n \times 2n$$
- Radical: Involves roots (e.g., $$x \sqrt{x}$$
- Linear: Involves constant rate of change (e.g., y=mx +by = mx + by=mx +b)
Understanding exponential vs radical vs linear helps distinguish between types of equations and their behaviors. Exponential growth, in particular, accelerates far more quickly.
Common Mistakes When Interpreting Base and Power
Even advanced learners make mistakes with exponents. Let’s address the most frequent ones.
Misinterpreting $$(-2)^4 = 16$$
This is a classic pitfall. The parentheses make all the difference:
$$(-2)^4 = 16$$
$$-2^4 = -16$$
Without parentheses, only the 2 is raised, and the negative sign applies afterward. Always consider order of operations and how parentheses affect the base and power in exponential formulas.
Forgetting Rules of Zero Power
Many forget that any non-zero number raised to the 0 power equals 1. That includes decimals, fractions, and negatives:
$$(-5)^0 = 1$$
$$\left(\frac{1}{2}\right)^0 = 1$$
Remember this zero exponent truth to avoid common errors.
How to Use an Exponent Calculator
An Exponent Calculator helps you quickly solve exponent problems without doing the math by hand. Here’s how to use it:
- Step 1: Enter the base (e.g., 4).
- Step 2: Enter the power or exponent (e.g., 3).
- Step 3: Click “Calculate” to get the result.
Example: If your base is 4 and your exponent is 3, the calculator shows:
- 4³ = 4 × 4 × 4 = 64
It’s perfect for checking homework, solving complex expressions, or learning how exponents work.
Save time and avoid mistakes with a reliable Exponent Calculator.
Base and Power in Real-World Applications
Exponential formulas aren’t just academic—they’re everywhere. You’ll find base and power in physics, chemistry, economics, and everyday tech.
Scientific Notation and Base 10
Scientific notation helps represent very large or small numbers compactly:
$$11.23 \times 10^{6} = 1,230,000$$
The base 10 is constant, and the power tells us how many places to move the decimal. This is widely used in science, engineering, and data storage.
Binary in Computing (Base 2)
Computers rely on binary, or base 2, to represent data. Every bit is a power of 2:
$$2^0 = 1, \quad 2^1 = 2, \quad 2^2 = 4$$
Understanding binary exponent use is essential for careers in programming, cybersecurity, and digital systems.
Exponential Growth Models (Base > 1)
Real-world exponential growth examples include:
- Population increase: $$P = P_0 (1 + r)^t$$
- Compound interest: $$A = P \left(1 + \frac{r}{n}\right)^{nt}$$
- Virus spread: Doubling rates over time
In each case, the base represents the growth rate, and the power reflects the time or repetitions. These base power growth models help forecast future scenarios.
Interactive Base and Power Quiz
Want to test your knowledge? Try these quick questions:
- What is $$323^{232}$$
- Simplify $$505^{050}$$
- True or False: $$(-4)^2 = -16$$
- What does a negative exponent mean?
- Which grows faster: linear or exponential?
These exponent MCQs reinforce key learning points and provide helpful review.
Printable Reference Table: Base & Power Rules
Here’s a handy chart you can print or save:
| Expression | Base | Power | Result |
| $$232^{323}$$ | 2 | 3 | 8 |
| $$10010^{0}100$$ | 10 | 0 | 1 |
| $$(3)^1$$ | 3 | 1 | 3 |
| $$5 – 2^{-2}$$ | 5 | -2 | 1/25 |
| $$xnx^nxn$$ | x | n | xⁿ |
This exponent cheat sheet is great for quick reference when solving math problems.
Understanding base and power in exponential formulas opens the door to a wide range of math and science applications. From solving equations to analyzing data growth, these two components work hand-in-hand to simplify complex ideas and power our digital world.
Whether you’re learning exponents for the first time or brushing up for an exam, always remember:
- The base is what you multiply.
- The power tells how often.
Together, they form the building blocks of exponential logic.
Frequently Asked Questions (FAQs)
What is the difference between base and power?
The base is the number being multiplied. The power tells how many times to multiply it. For example, in 434^343, 4 is the base and 3 is the power.
Can the base be a variable like x?
Yes! Algebra often uses variables as bases. Examples include:
$$x^2a^{b}x^n$$
These are common in equations and functions.
Is power always a whole number?
No. Powers can be:
- Negative: $$3^{-2} = \frac{1}{3^2} = \frac{1}{9}$$
- Fractional: $$9^{\frac{1}{2}} = \sqrt{9} = 3$$
- Decimal: $$100^{0.5} \approx 3.16$$
These are known as non-integer exponents.
What is the base in scientific notation?
It’s always 10. Scientific notation expresses numbers as a decimal multiplied by a power of 10:
$$2.5 \times 10^3 = 2,500$$
Why does anything to the power of 0 equal 1?
Mathematically, it’s defined that way. When you reduce exponents step-by-step, anything⁰ equals 1 by logical progression. It’s a foundational math rule.
How do parentheses affect base and exponent?
Parentheses change the scope of what’s raised. Compare:
$$(-3)^2 = 9$$
$$-3^2 = -9$$
This difference is key to proper exponent notation.
Can both base and exponent be variables?
Yes. Advanced math often uses expressions like:
$$xyx^yxy$$
$$aba^bab$$
These appear in calculus, statistics, and computer science.
Leave a Reply