Have you ever stared at the word “logarithm” in a math textbook and instantly felt confused or intimidated? You’re not alone. For many students and even adults, logarithms can seem like a complex math concept only meant for scientists or engineers.
But here’s the truth: logarithms are incredibly useful in everyday life and are much simpler than they first appear. From measuring earthquake intensity to calculating interest rates and data growth, logarithms play a behind-the-scenes role more often than you think. And thanks to modern tools like a log calculator, working with logarithms is easier than ever.
Imagine being able to confidently solve log equations or understand graphs in seconds, even if you’re not a math expert. This guide will explain what a logarithm is, how it relates to exponents, how to apply log rules, and how to use calculators to make your work quick and simple. Whether you’re a student, a curious learner, or preparing for an exam, this beginner-friendly guide will make logs finally click.
Ready to learn logarithms? Let’s break them down step-by-step so you can understand and apply them with confidence.
What Is a Logarithm in Math?
A logarithm is the opposite of an exponent. When you see something like $$2^{3} = 8$$, the logarithmic form asks: “To what power must 2 be raised to get 8?” The answer is 3. So, $$\log_b x = y$$ which means $$b^{y} = x$$.
In simpler terms, a logarithm in math helps you find the exponent that turns one number into another. It’s written as:
Where:
- b is the log base
- x is the number you’re taking the log of
- y is the exponent
Understanding this exponential relationship is the foundation of logarithms.
Types of Logarithms
There are several types of logarithms, each defined by its base. Understanding these different types is key to knowing which one to use depending on the problem you’re solving—whether it’s in science, finance, or computer science.
- Common Logarithm (Base 10)
This is written as log x, where the base is implicitly 10. It’s widely used in fields like physics, chemistry, and engineering when dealing with data that spans multiple orders of magnitude, such as sound levels or pH values.
Example:
$$[
\log 100 = 2 \quad \text{because} \quad 10^2 = 100
]$$
Most calculators use base 10 by default when you press the log button. This makes common logs particularly useful for quick manual calculations.
- Natural Logarithm (Base e)
This type of logarithm uses Euler’s number (e ≈ 2.718) as the base and is written as ln x. It’s especially important in higher mathematics, particularly calculus, due to its natural properties when dealing with rates of change, exponential growth, or decay.
Example:
- lne=1
You’ll often see natural logarithms used in population growth models, radioactive decay, and compound interest calculations, where continuous growth is involved.
- Binary Logarithm (Base 2)
The binary logarithm, written as log , is crucial in computer science. Since digital systems operate using binary (0s and 1s), this type of log helps analyze algorithms, data storage, and computational complexity.
Example:$$[
\log_{2} 8 = 3 \quad \text{because} \quad 2^3 = 8
]$$
This form of logarithm is commonly used when calculating time or space efficiency in coding and algorithm design.
Logarithm Rules and Properties
To work with logarithms efficiently, it’s important to master a few fundamental rules. These logarithm rules allow you to simplify complex expressions, solve equations, and switch between different forms with ease. Whether you’re solving homework problems or using a log calculator, these properties are essential tools in your math toolkit.
Product Rule
Formula: $$[
\log_{a}(xy) = \log_{a}(x) + \log_{a}(y)
]$$
Example: $$[
\log_{3}(9 \times 27) = \log_{3}(9) + \log_{3}(27) = 2 + 3 = 5
]$$
.
Quotient Rule
Formula: $$[
\log_{a}\left(\frac{x}{y}\right) = \log_{a}(x) – \log_{a}(y)
]$$
Example: $$[
\log_{2}\left(\frac{16}{4}\right) = \log_{2}(16) – \log_{2}(4) = 4 – 2 = 2
]$$
Power Rule
Formula: $$[
\log_{a}(x^n) = n \cdot \log_{a}(x)
]$$
Example: $$[
\log_{5}(25^3) = 3 \cdot \log_{5}(25) = 3 \cdot 2 = 6
]$$
Change of Base Rule
Formula: $$[
\log_{a}(b) = \frac{\log(b)}{\log(a)}
]$$
Why Useful: Lets you calculate logs of any base using a standard log calculator.
How to Use a Log Calculator
Step-by-Step Guide
- Step 1: Identify the Base: Most calculators default to base $$ [\log_{a}(b) = \frac{\log_{10}(b)}{\log_{10}(a)}]$$
- Step 2: Enter the Number: Type the value you want to find the log of.
- Step 3: Switch Bases (if needed): Use the change of base rule for non-standard bases.
Logarithm Formulas You Must Know
To solve logarithmic expressions quickly and accurately, it’s essential to remember a few key formulas. These core rules simplify calculations, help solve equations, and are frequently used in algebra, calculus, and real-world applications. Think of them as your go-to shortcuts when working with logarithms—whether by hand or using a log calculator.
| Formula | Example | Use Case |
| $$[ \log_{a}(1) = 0 ]$$ | $$[ \log_{7}(1) = 0 ]$$ | Simplifying equations |
| $$[ \log_{a}(a) = 1 ]$$ | $$[ \log_{5}(5) = 1 ]$$ | Validating solutions |
| $$[ a^{\log_{a}(x)} = x ]$$ | $$[ 10^{\log(100)} = 100 ]$$ | Solving exponential equations |
Solving Logarithmic Equations (with Examples)
- Problem: Solve $$[\log_{4}(x) = 3]$$
Solution: Convert to exponential form: $$[
4^{3} = x \quad \rightarrow \quad x = 64
]$$
.
- Problem: Solve $$[2 \times \log_{3}(x) = 6]$$
Solution: Divide by $$[
2 \quad \rightarrow \quad \log_{3}(x) = 3 \quad \rightarrow \quad x = 3^{3} = 27
]$$
Real-Life Applications of Logarithms
1. Science: pH scale (logarithmic measure of acidity).
2. Finance: Calculating compound interest.
3. Engineering: Decibel levels for sound intensity.
History of Logarithms
Logarithms were invented by Scottish mathematician John Napier in 1614 as a way to simplify complex calculations. Before calculators existed, multiplying large numbers was time-consuming and error-prone. Napier’s logarithmic tables turned multiplication into simple addition, making calculations faster and more accurate.
This breakthrough revolutionized fields like astronomy, navigation, and engineering, where precision and speed were critical. Later, Henry Briggs refined the concept by introducing common logarithms (base 10), which made the method even more practical and widely used.
The invention of logarithms marked a turning point in mathematical history, laying the groundwork for modern computation long before electronic calculators.
Common Errors and Misconceptions
- Mistake: Assuming $$[\log(a b) = \log(a) + \log(b)]$$
Truth: Only works for products $$(log(ab) = log(a) + log(b))$$.
- Mistake: Ignoring domain restrictions $$(log(0) or log(-1)$$ are undefined).
Final Thoughts: Why Learn Logarithms?
So, why learn logarithms? Because they unlock deep mathematical understanding and have real applications in science, finance, and tech. They’re also critical for higher-level studies, including algebra, calculus, and data science.
With the help of a log calculator, learning and applying logs becomes less intimidating and more accessible. Whether you’re solving equations, interpreting data, or preparing for exams, mastering logarithms gives you an edge.
Now that you know what a logarithm is, how about practicing a few examples using your favorite calculator tool? You might just find logarithms more interesting than you expected.
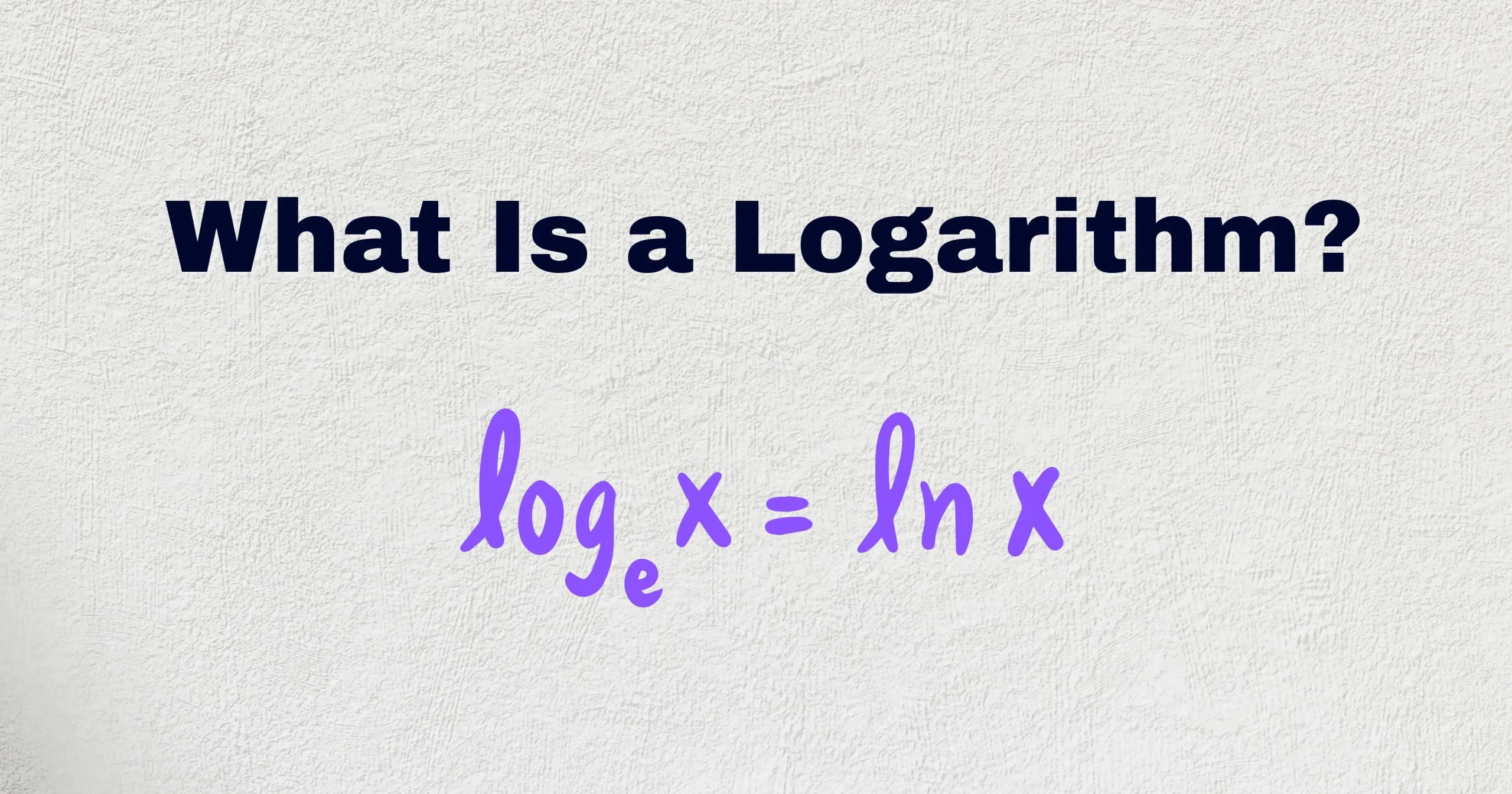
Leave a Reply