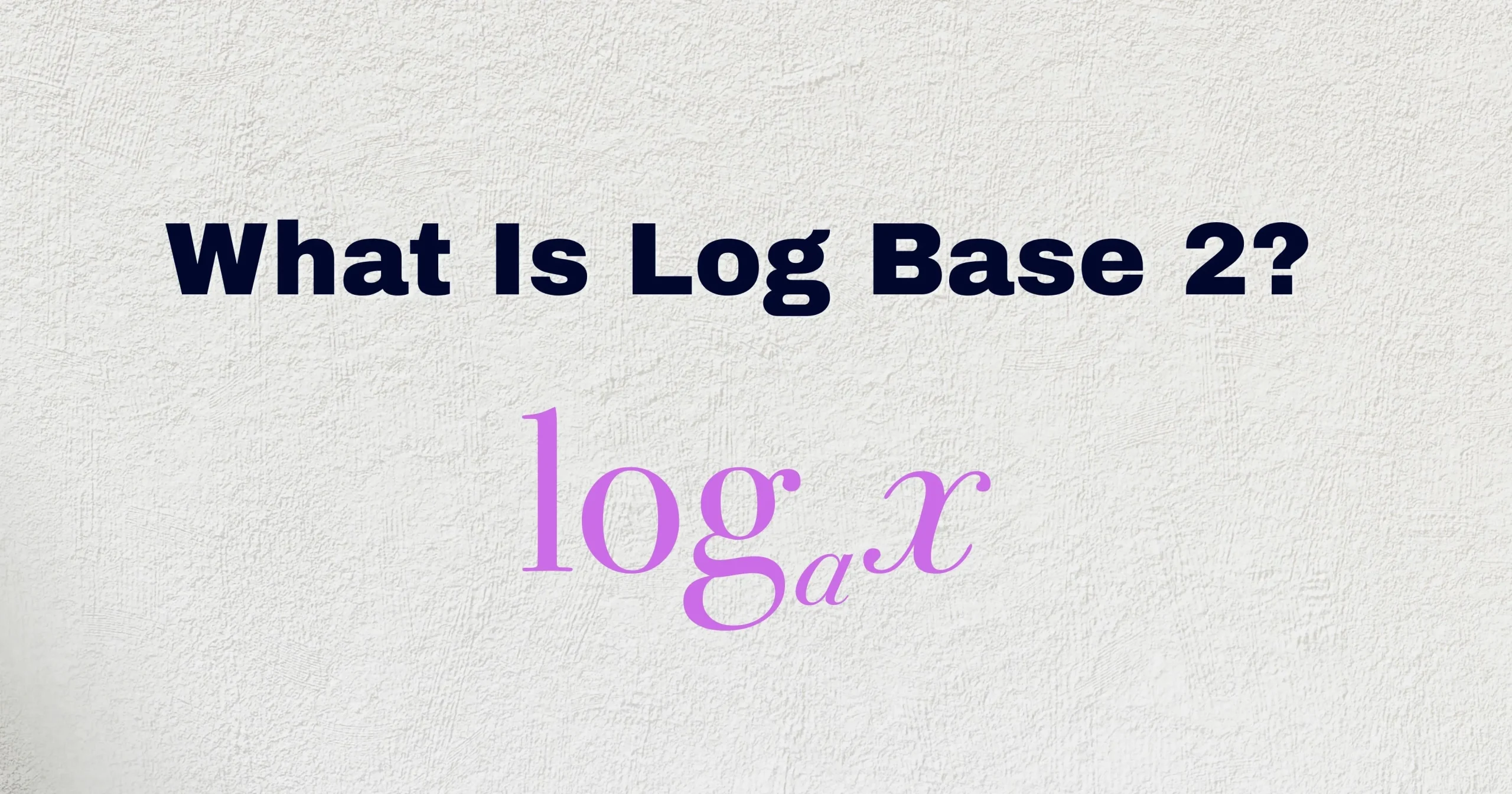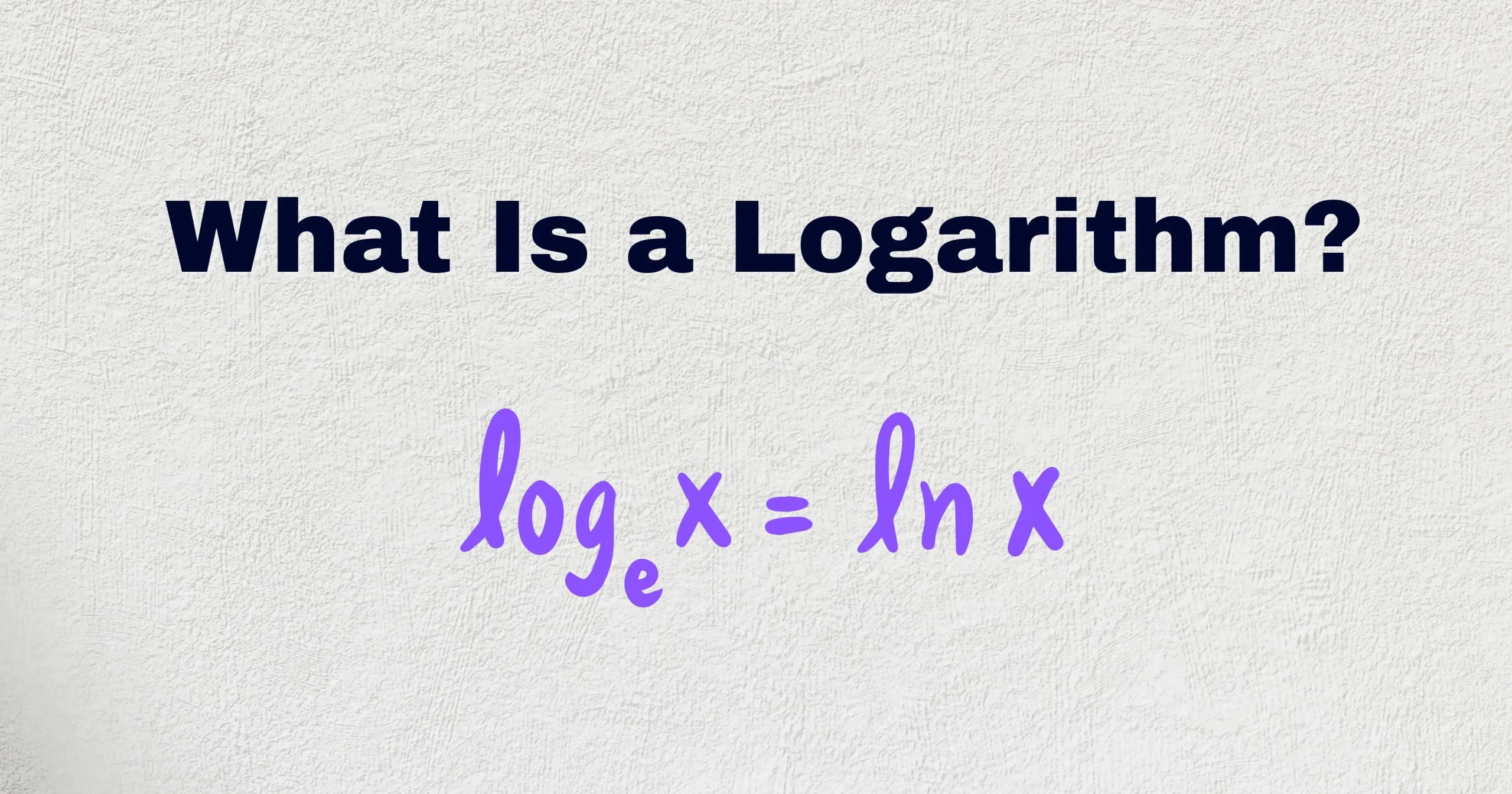Calculus Hub BLog

Blog

  • What Is Log Base 2? Understand Logarithms in Binary Systems

    What Is Log Base 2? Understand Logarithms in Binary Systems

    In computers, log base 2 helps us understand how data is stored and used. It shows how many times we need to multiply 2 to get a number.

    If you’ve seen file sizes (like KB or MB), used binary numbers (just 0s and 1s), or learned about algorithms, log base 2 is working behind the scenes.

    In this guide, you’ll learn:

    • What log base 2 means
    • How to use its formula
    • Where it’s used in real life
    • Some easy examples to practice

    Let’s make it simple and clear, step by step!

    Definition of Logarithm

    • logₐ(x) = y  ➔  aⁿ = x

    Before we learn about log base 2, let’s understand what a logarithm is. A logarithm tells us how many times we need to multiply a number (called the base) to get another number.

    Example:

    • log₂(8) = 3 ➔ because 2³ = 8

    This function is called the logarithmic function, and it has three components:

    • The base (a)
    • The input (x)
    • The output or exponent (y)

    Common bases include:

    • Base 10: log₁₀(x) (common logarithm)
    • Base e: ln(x) (natural logarithm)
    • Base 2: log₂(x) (binary logarithm)

    Logarithms are inverse operations of exponents. So, if 2ⁿ = x, then log₂(x) = y.

    Understanding Log Base 2 in Simple Terms

    To understand log base 2, imagine folding a sheet of paper. If you fold it once, you get 2 layers. Fold again: 4 layers. Fold again: 8 layers. The number of folds = log₂(number of layers).

    Real-life example:

    • You have 16 pieces of chocolate. How many times do you need to divide them in half to get 1 piece?

    Answer: log₂(16) = 4

    Another scenario: You want to know how many times you can split a group of people in half before ending up with individuals. That number is log₂(group size).

    This shows the log base 2 meaning: how many times do you divide or multiply by 2 to reach a target number.

    Formula of Log Base 2

    The log base 2 formula is fundamental for solving problems involving binary growth or division. It’s written as:

    • log₂(x) = y  ⇔  2ʸ = x

    This equation tells us: “To what power must 2 be raised to get the number x?” In simpler terms, you’re finding how many times you can multiply 2 to reach a certain value.

    Examples:

    • log₂(32) = 5 → Because 2⁵ = 32
    • log₂(64) = 6 → Because 2⁶ = 64
    • log₂(1) = 0 → Because 2⁰ = 1
    • log₂(0.5) = -1 → Because 2⁻¹ = 0.5

    This formula is especially helpful when working with powers of two, which frequently appear in computing, binary systems, and algorithm analysis. You can also rearrange this formula to solve exponential equations like:

    • 2ʸ = 128  ⇨  log₂(128) = y  ⇨  y = 7

    Change of Base Formula for Log Base 2

    Most basic calculators don’t have a direct log base 2 button. But you can still calculate it using either common logarithms (base 10) or natural logarithms (base e). Here’s how:

    Using Base 10:

    $$\log_2(x) = \frac{\log_{10}(x)}{\log_{10}(2)}$$

    Using Natural Log (ln):

    $$\log_2(x) = \frac{\ln(x)}{\ln(2)}$$

    Both methods give you the same result, and they’re crucial when working with decimal or non-exact values. For example:

    • log₂(20)

    $$\frac{\log_{10}(20)}{\log_{10}(2)}$$

    $$\frac{1.3010}{0.3010} \approx 4.32$$

    • log₂(5)

    $$\frac{\ln(5)}{\ln(2)}$$

    $$\frac{1.6094}{0.6931} \approx 2.32$$

    The change of base log formula is a powerful trick for solving any log base 2 problem, even when you’re limited to basic scientific tools.

    Properties of Log Base 2

    The properties of log base 2 are essential for simplifying and solving logarithmic expressions. These rules help break down complex problems into manageable parts, especially useful in programming, mathematics, and data science.

    1. Product Rule

    • log₂(ab) = log₂(a) + log₂(b)

    When two values are multiplied inside the log, you can split them into the sum of two separate logs.

    Example:

    • log₂(8 × 4) = log₂(32) = 5
    • log₂(8) + log₂(4) = 3 + 2 = 5

    2. Quotient Rule

    $$\log_2\left(\frac{a}{b}\right) = \log_2(a) – \log_2(b)$$

    If you’re dividing inside the log, convert it into a subtraction of two logs.

    Example:

    $$\log_2\left(\frac{16}{2}\right) = \log_2(8) = 3$$

    $$\log_2(16) – \log_2(2) = 4 – 1 = 3$$

    3. Power Rule

    If the input is raised to a power, bring that power in front of the log as a multiplier.

    Example:

    • log₂(4³) = log₂(64) = 6
    • 3 × log₂(4) = 3 × 2 = 6

    These log base 2 properties help simplify logarithmic expressions, making it easier to handle exponential growth or decay in real-world problems. They are especially useful in:

    • Algorithm complexity analysis
    • Binary tree depth calculations
    • Data compression and cryptography

    By mastering these rules, you’ll have a faster, more efficient way to approach both theoretical and practical problems involving logarithms.

    Log Base 2 to Exponential Form

    Converting a logarithmic expression to its exponential form is a key skill in both math and computer science. Specifically, for log base 2, the conversion helps simplify calculations and understand powers of 2, a common base in binary and algorithm design.

    The general form of a log base 2 equation is:

    • log₂(x) = y

    This can be rewritten in exponential form as:

    • 2ʸ = x

    This means that the logarithm tells you the exponent you must raise 2 to in order to get x.

    Example:

    • log₂(8) = 3 ➝ 2³ = 8

    This shows that 2 raised to the power of 3 equals 8.

    This conversion is especially useful in algebra, data structures, coding algorithms (like binary search), and analyzing time complexity (e.g., O(log₂ n)) in computer science.

    Understanding this relationship helps make complex logarithmic expressions more intuitive and manageable.

    Log Base 2 Table (Values from 1 to 100)

    Here is a reference table showing log base 2 values for numbers from 1 to 100. This can help you quickly estimate or verify results in binary calculations, algorithms, and logarithmic equations without needing a calculator.

    xlog₂(x)
    10.000
    21.000
    42.000
    83.000
    164.000
    325.000
    646.000
    100~6.643

    Practice Question

    Test your understanding with these log base 2 practice problems. Use logarithmic rules (product, quotient, power) and estimation for approximations:

    1. log₂(128) = ?
    2. log₂(1/8) = ?
    3. log₂(2³ × 2²) = ?
    4. log₂(256) = ?
    5. log₂(0.25) = ?
    6. log₂(512) = ?
    7. log₂(0.125) = ?
    8. log₂(2⁶ / 2²) = ?
    9. log₂(10) ≈ ? (approximate)
    10. log₂(3.5) ≈ ? (approximate)
    11. log₂(64) = ?
    12. log₂(2⁵) = ?
    13. log₂(1) = ?
    14. log₂(2⁰.⁵) = ? (hint: square roots)
    15. log₂(100) ≈ ? (approximate)

    Common Mistakes with Log Base 2

    When learning log base 2, it’s easy to make small mistakes. Here are some to watch out for:

    • Using the wrong base: Don’t mix up log base 2 with log base 10 (log) or natural log (ln). Always check you’re using base 2, especially in coding or binary problems.
    • Wrong input: You can only use log base 2 with positive numbers.

    Example: log₂(0) or log₂(−5) doesn’t work.

    • Formula errors: Don’t forget the correct rules:
    • log₂(a × b) = log₂(a) + log₂(b)
    • log₂(a ÷ b) = log₂(a) − log₂(b)
    • log₂(aⁿ) = n × log₂(a)
    • Calculator issues: Some calculators don’t have log base 2. Use this formula:

    $$\log_2(x) = \frac{\log_{10}(x)}{\log_{10}(2)}$$

    Log Base 2 Calculator

    A log base 2 calculator is a helpful tool for quickly finding the logarithm of any positive number with base 2. It’s especially useful for students, programmers, and anyone working with binary systems or exponential functions.

    How to Use Log Base 2 Calculator

    1. Enter a positive number into the input field.
    2. Click the “Calculate” button to process the input.
    3. View the result of log₂(x) displayed instantly on the screen.

    This online calculator supports both whole numbers and decimals, providing fast and accurate outputs without manual calculation. It reduces the risk of mistakes and is ideal for assignments, coding, or checking complex expressions in seconds.

    Real-World Applications of Log Base 2

    Log base 2 isn’t just something you learn in school—it’s used in many real-world technologies, especially in computers and data systems.

    In Computer Science:

    • Binary Search: Used to find things quickly in sorted lists. It takes about log₂(n) steps.
    • Binary Trees: Log base 2 helps figure out how tall a tree is, which makes searches faster.
    • File Sizes: Computers use powers of 2 (like 2, 4, 8, 16…), so log₂ helps measure how many bits are needed to store data.
    • Sorting Algorithms: Fast sorting methods like merge sort use log base 2 in their time calculations.

    In Information Theory:

    • Entropy (Information Amount): Log₂ tells how much information is in a message, measured in bits.
    • Data Compression: Used to shrink file sizes without losing important info.
    • Internet Speed (Bit Rate): Log base 2 helps figure out how many bits are needed to send or receive data.

    In Science and Engineering:

    • Sound and Images: Formats like MP3 and JPEG use log base 2 to make files smaller.
    • DNA and Genetics: Scientists use log-based math to work with large amounts of genetic data.
    • Log base 2 is all around us, in apps, music, videos, the internet, and even science labs!

    FAQs on Log Base 2

    What is log base 2 in algebra?

    In algebra, log base 2 helps solve exponential equations involving powers of 2. For instance, if log₂(x) = 3, then x = 2³ = 8.

    How do you solve log base 2 equations?

    Rearrange them into exponential form: log₂(x) = y becomes x = 2ⁿ. Then calculate the power to get your solution.

    What is the derivative of log base 2?

    The derivative of $$\frac{d}{dx} \log_2(x) = \frac{1}{x \cdot \ln(2)}$$. It is used in calculus to determine rates of change.

    Is log base 2 the same as binary log?

    Yes, binary logarithm is another name for log base 2. It’s commonly used in computer science to measure bits.

    Can log base 2 be negative?

    The result can be negative when the input is between 0 and 1. For example, log₂(0.5) = -1.

    What is log base 2 of 0?

    It is undefined because no power of 2 gives 0. Logarithms are only defined for positive real numbers.

    How is log base 2 used in data structures?

    It’s used to determine the height of binary trees or complexity of algorithms like binary search. These structures are logarithmic in nature.

    Is log base 2 used in everyday life?

    Yes, especially in digital devices, data compression, and even music encoding. It helps with calculating storage and data transmission rates.

    What if my calculator doesn’t have log base 2?

    Use the change of base formula: $$\log_2(x) = \frac{\log_{10}(x)}{\log_{10}(2)}$$. Most scientific calculators support base 10 logs.

    Why is log base 2 important in algorithms?

    Because many algorithms work by dividing data in halves, making their complexity logarithmic. It helps measure efficiency and performance.

  • Beginner’s Guide to Using a Hex Calculator for Programming Tasks

    Hexadecimal values are a common part of many programming tasks. Whether you’re debugging, doing low-level programming, or just exploring memory addresses, using a hex calculator for programming is essential. This guide to using a Hex Calculator will walk you through the basics and help you become confident in working with hex values in real-world coding scenarios.

    What Is a Hexadecimal Number System?

    The hexadecimal number system (often shortened to hex) is a base-16 system. Unlike the decimal system, which uses 10 digits (0–9), hex uses 16 symbols: the numbers 0 through 9 and the letters A through F. Each digit represents a value from 0 to 15.

    Hex is often used in computing because it offers a more human-readable form of binary. For example, instead of writing 11111111 in binary, you can simply use 0xFF in hexadecimal.

    Hex values are vital for programmers, especially in memory manipulation, low-level code, and color codes in web design. Following this guide to using a Hex Calculator for programming will save time and reduce errors.

    Why Programmers Use Hex

    One of the main reasons why hex is used in coding is its efficiency. Every hex digit represents four binary digits (bits), making it much easier to read and write large binary numbers. For instance, instead of writing 11001011, you can use 0xCB.

    Hex is also used to represent memory addresses clearly. In languages like C and assembly, hex values are commonly used to define locations in RAM or EEPROM. Additionally, hex in embedded systems plays a major role because hardware typically interfaces with binary and hexadecimal formats.

    Hex vs Binary vs Decimal

    It’s important to understand the difference between hex vs binary vs decimal. All three are numeral systems:

    • Binary: Base-2, uses 0 and 1
    • Decimal: Base-10, uses 0 through 9
    • Hexadecimal: Base-16, uses 0–9 and A–F

    A simple comparison table:

    DecimalBinaryHex
    101010A
    25511111111FF
    161000010

    Each system has its use. Decimal is human-friendly, binary is used internally by machines, and hex is a readable format for binary data. Using a hex calculator for programming helps convert and compare these formats easily.

    Examples of Hex Numbers

    Some typical examples of hex in programming include values like 0x1A, 0xFF, or 0x00FF23. These are often seen in hardware register configurations, color codes, and debugging output.

    For instance:

    int color = 0xFF5733;

    Here, 0xFF5733 defines a color in hexadecimal format for use in web development or GUI programming.

    Introduction to Hex Calculators

    A hex calculator is a digital tool that simplifies operations involving hexadecimal numbers. Unlike standard calculators, hex calculators support base conversions and logic operations directly related to programming tasks.

    So, what is a hex calculator exactly? It’s a hexadecimal computation tool that lets you perform hex arithmetic, conversions, and bitwise operations. Whether you’re working with a microcontroller or decoding crash logs, a calculator for hex values is incredibly helpful.

    Types of Hex Calculators

    There are various types of hex calculator tools available today:

    • Online hex calculators – Easily accessible and free (e.g., RapidTables, CalculatorSoup)
    • Mobile hex apps – Useful on-the-go for Android and iOS
    • Hardware scientific calculators – Some advanced models support hex directly

    Depending on your workflow, you might choose an online hex calculator for speed or a mobile hex app for convenience.

    User Interface Basics

    Most hex calculators have a simple interface. Understanding the hex calculator layout can make a big difference. Typically, you’ll see:

    • Buttons for hex digits (0–9 and A–F)
    • Options to switch between decimal, binary, and hexadecimal
    • Logical operation buttons (AND, OR, XOR)

    By learning these interface functions, you’ll navigate and use your calculator more efficiently.

    Basic Functions You Can Perform with a Hex Calculator

    The core hex calculator operations include:

    • Addition (e.g., 0x1A + 0x2B = 0x45)
    • Subtraction
    • Hex to decimal conversion
    • Bitwise logic operations like AND, OR, XOR

    These functions are vital for tasks like data encoding, configuration registers, and debugging. Whether you’re doing hex math operations or format conversion, your calculator makes it easy.

    Hex to Decimal Conversion

    To convert hex to decimal, input a value like 0x1F into your hex calculator. It will output 31 in decimal. This is a simple example of base conversion that programmers perform daily.

    Decimal to Hex Conversion

    For decimal to hex conversion, input 100 in decimal mode, and the calculator will show 0x64. This is helpful when setting buffer sizes or working with register addresses.

    Logical Operations: AND, OR, XOR

    Bitwise hex operations are commonly needed in embedded programming. For example:

    0x0F AND 0xF0 = 0x00

    These logical hex operations help control bits at a granular level.

    How Hex Helps in Low-Level Programming

    Using hex in low-level programming is crucial. In embedded systems, values are often represented in hex for efficiency and clarity. Registers, memory, and machine code often rely on hexadecimal values.

    Memory Addressing

    Hex values make it easier to understand and work with memory. For instance, 0x0040FF20 is more readable than the equivalent binary. This helps when analyzing hex memory addresses or debugging RAM usage.

    Color Codes in Web Development

    Hex is not just for low-level coding. In web development, hex color codes define colors. For example:

    color: #FF5733;

    This is a red-orange tone. These HTML color hex values are common in front-end design.

    Debugging Output

    When programs crash, logs often show hex dumps. Interpreting this data helps you find the source of the error. Knowing hex in debugging is a must-have skill.

    Performing Arithmetic with Hex Values

    Doing hex math operations manually can be tricky, which is why calculators help so much. You can add, subtract, and multiply hex values just like decimal, but you must understand the rules of base-16 math.

    Carrying and Borrowing in Hex

    When adding A + 5, you get F, but A + 6 results in a carry because the result is 10 (in hex: 0x10). Learning to carry in hexadecimal math is key for accurate results.

    Overflow and Limits

    In 8-bit systems, values are limited. For example, 0xFF + 1 becomes 0x100, an overflow condition. This is vital when working with register limits or handling hex overflow examples.

    Common Mistakes to Avoid When Using Hex

    Many beginners make simple but critical mistakes while using a hex calculator for programming. Here’s what to watch out for.

    Confusing Hex with Decimal

    The number 10 in decimal is not the same as 0x10 in hex. Always watch for hex vs decimal confusion when reading code or configuring hardware.

    Ignoring Prefixes

    Some programming tools need a 0x prefix before hex values. Without it, you may get unexpected results. Understand the hex prefix importance to avoid bugs.

    When to Use a Hex Calculator in Programming

    Here are the most common use cases for hex calculator in real-world programming:

    • Setting memory addresses
    • Reading debug logs
    • Defining color codes in web design
    • Performing bitwise operations
    • Optimizing data structures in embedded systems

    Knowing the best time to use a calculator can streamline your workflow.

    Visual Tools and Emulators with Built-In Hex Calculators

    Some programming IDEs and development tools include built-in hex calculator support. These tools let you visualize memory in hex and do operations without switching tools.

    Arduino, Microcontroller IDEs

    Many IDEs for microcontrollers, like Arduino or AVR Studio, support hex input/output for ports, memory, and configuration registers. This helps with hex use in Arduino projects.

    Emulator Debuggers

    In emulators, using hex during runtime debugging can show you memory values at breakpoints. You might see:

    Memory[0x00FF] = 0x34   

    Learning how to debug with hex helps find bugs in assembly and low-level C programs.

    Mastering the use of a hex calculator for programming opens the door to more efficient, accurate, and advanced development. Whether you’re debugging embedded systems, managing color values, or doing low-level code, hex will be your daily companion. Keep practicing with tools, understand the math, and you’ll become a pro in no time.

    FAQs: Hex Calculators for Beginners

    What is a hex calculator used for in programming?

    A hex calculator helps with arithmetic, conversions, and logic operations on hexadecimal numbers. It’s crucial for debugging, embedded systems, and memory tasks.

    Can I use it to convert between binary and hex?

    Yes! Most calculators support converting binary to hex. For example, binary 1010 becomes hex A.

    Is hex still used in modern programming?

    Absolutely. It’s common in modern low-level programming, especially in system-level, embedded, and hardware control projects.

    Are online hex calculators reliable?

    Yes, but use trusted hex tools like RapidTables, CalculatorSoup, or HexEd.it. These are secure calculator websites used by professionals.

    What does “0x” mean in hex notation?

    The 0x prefix tells the system that the number is in hex. It’s part of standard hex identifier syntax.

  • Top 15 Common Mistakes with Exponents

    Understanding exponents is essential in both academic mathematics and real-world problem-solving. Yet, they often confuse students and even professionals. Why? Because exponents introduce new layers of abstraction that build upon basic arithmetic rules—and it’s easy to misapply them.

    From calculator errors to order of operations, exponent errors can derail calculations quickly. In this post, we’ll break down the top 15 common mistakes with exponents, explain why they happen, and help you avoid them with simple examples and solutions.

    1. Confusing Multiplication with Exponentiation

    One of the most frequent exponent mistakes students make is thinking 2 × 3 is the same as 2³.

    But let’s clear this up:

    • 2 × 3 = 6 (just multiplication)
    • 2³ = 8 (2 × 2 × 2)

    These are totally different operations. Multiplication involves repeated addition, while exponentiation involves repeated multiplication.

    📱 Try this on your calculator to visualize the difference!

    2. Ignoring Negative Exponents

    Another big misconception: “Can you have a negative exponent?” Yes! And here’s how it works:

    • $$[x^{-2} = \frac{1}{x^2}]$$
    • Example: $$3⁻² = 1/3² = 1/9$$

    The negative sign means you’re taking the reciprocal—not that the result is negative.

    Ignoring this rule can mess up your entire equation, especially in physics and engineering where precision is key.

    3. Forgetting Order of Operations (PEMDAS)

    Let’s face it—PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) trips up everyone at some point.

    Here’s a classic mistake:

    • Problem: 2 + 3² × 2
    • Wrong: (2 + 3)² × 2 = 25 × 2 = 50
    • Correct: 3² × 2 = 9 × 2 = 18; then 2 + 18 = 20

    Exponents must come before multiplication or addition. Period.

    4. Misusing Zero as an Exponent

    Students often think:

    • x⁰ = 0

    But actually:

    • x⁰ = 1 (for x ≠ 0)

    However, 0⁰ is undefined—a common calculator error.

    📌 Remember: Any non-zero number raised to the power of 0 equals 1.

    5. Misinterpreting Scientific Notation

    If you see 5E3 on your TI-84, don’t panic. That just means:

    • 5 × 10³ = 5000

    But many misread “E” as a variable instead of part of scientific notation.

    ⚠️ Watch out: Using “E” incorrectly in calculations can throw off your answers by orders of magnitude.

    6. Misplacing Parentheses

    This is a calculator classic:

    • -2² = -4 (squared first, then apply minus)
    • (-2)² = 4 (square the entire number, including the negative)

    Big difference. Parentheses matter more than you think.

    7. Applying Laws of Exponents Incorrectly

    Laws of exponents are powerful—but only if used correctly.

    Incorrect:

    • 2³ × 3³ ≠ 6⁶

    Correct:

    • You can only combine exponents if the base is the same:
      $$a^m \times a^n = a^{m+n}$$

    Use Exponent calculator to verify if unsure!

    8. Misunderstanding Fractional Exponents

    What does $$[
    x^{\frac{1}{2}}
    ]$$

    mean?

    It’s the same as the square root of x:

    • $$[x^{\frac{1}{2}} = \sqrt{x}]$$

    Other fractional exponents follow the same logic:

    • $$[x^{\frac{1}{3}} = \sqrt[3]{x}]$$

    So, don’t confuse them with decimals—they represent roots.

    9. Incorrect Use of Exponent Rules in Binomials

    One of the most common mistakes:

    • (a + b)² ≠ a² + b²

    Correct:

    • (a + b)² = a² + 2ab + b²

    Calculator check:

    • Try with a = 2, b = 3
    • Left: (2 + 3)² = 25
    • Right: 2² + 3² = 13 ❌

    10. Forgetting to Apply Exponent to Entire Base

    Mistake:

    • (3x)² ≠ 3x²

    Correct:

    • (3x)² = 9x²

    You must square everything inside the parentheses.

    This error is often seen in algebraic simplifications. Always distribute the exponent properly.

    11. Misusing Negative Base Exponents

    Looks similar, but the position of parentheses changes everything:

    • $$(-2)^4 = 16$$
    • $$-2^4 = -16$$

    One is positive, the other is negative. Parentheses change the base, and the sign goes with it.

    12. Dropping Exponents During Simplification

    You’re simplifying an expression, and somewhere—the exponent vanishes.

    Example:

    • Starting with x² + 3x², some mistakenly simplify to 4x ❌

    Correct:

    • x² + 3x² = 4x² ✅

    Never drop exponents unless a rule tells you to!

    13. Ignoring Units in Exponential Applications

    Real-world problems involve units:

    • Area = length²
    • Volume = length³

    If you forget units, your result may be numerically right but practically useless.

    Example:

    • 5 m² ≠ 5 m
    • Growth rate (% per year) involves exponential models.

    14. Incorrect Conversion Between Decimal & Exponential Forms

    Knowing how to go from:

    • $$[0.0005 \rightarrow 5 \times 10^{-4}]$$

    And back again is crucial, especially in scientific and engineering contexts.

    Your calculator might help, but only if you know what to input and interpret.

    15. Overgeneralizing Exponent Rules

    Here’s a trap:

    • $$a^m + a^n \ne a^{m+n}$$

    This is never true. Only multiplication lets you add exponents:

    • $$a^m \times a^n = a^{m+n}$$ ✅

    Adding powers? You’re stuck with:

    • $$a^m + a^n$$ (just leave it as-is unless factoring)

    How Calculators Help Avoid These Mistakes

    Modern graphing calculators like the TI-84 or online tools such as Desmos can prevent most of these exponent errors.

    ✔ They show parentheses clearly
    ✔ They interpret operator precedence accurately
    ✔ They provide scientific notation and even root symbols

    Pro tip: Use the calculator’s exponent function instead of typing “^” manually to avoid input errors.

    FAQs About Exponent Errors and Calculators

    Q1: Why does my TI-84 show “E”?
    That “E” is shorthand for scientific notation. Example: $$[
    1.2\text{E}4 = 1.2 \times 10^{4}
    ]$$

    Q2: How do you solve a problem with a negative exponent?
    Rewrite it using a reciprocal:

    • $$[x^{-n} = \frac{1}{x^n}]$$

    Q3: What’s the fastest way to simplify exponents on a calculator?
    Use parentheses for clarity and the “^” or exponent button. For roots, use fractional exponents like $$[
    x^{\frac{1}{2}}
    ]$$

  • What Is a Logarithm? Beginner’s Guide to Using a Log Calculator

    What Is a Logarithm? Beginner’s Guide to Using a Log Calculator

    Have you ever stared at the word “logarithm” in a math textbook and instantly felt confused or intimidated? You’re not alone. For many students and even adults, logarithms can seem like a complex math concept only meant for scientists or engineers.

    But here’s the truth: logarithms are incredibly useful in everyday life and are much simpler than they first appear. From measuring earthquake intensity to calculating interest rates and data growth, logarithms play a behind-the-scenes role more often than you think. And thanks to modern tools like a log calculator, working with logarithms is easier than ever.

    Imagine being able to confidently solve log equations or understand graphs in seconds, even if you’re not a math expert. This guide will explain what a logarithm is, how it relates to exponents, how to apply log rules, and how to use calculators to make your work quick and simple. Whether you’re a student, a curious learner, or preparing for an exam, this beginner-friendly guide will make logs finally click.

    Ready to learn logarithms? Let’s break them down step-by-step so you can understand and apply them with confidence.

    What Is a Logarithm in Math?

    A logarithm is the opposite of an exponent. When you see something like $$2^{3} = 8$$, the logarithmic form asks: “To what power must 2 be raised to get 8?” The answer is 3. So, $$\log_b x = y$$ which means $$b^{y} = x$$.

    In simpler terms, a logarithm in math helps you find the exponent that turns one number into another. It’s written as:

    Where:

    • b is the log base
    • x is the number you’re taking the log of
    • y is the exponent

    Understanding this exponential relationship is the foundation of logarithms.

    Types of Logarithms

    There are several types of logarithms, each defined by its base. Understanding these different types is key to knowing which one to use depending on the problem you’re solving—whether it’s in science, finance, or computer science.

    1. Common Logarithm (Base 10)

    This is written as log x, where the base is implicitly 10. It’s widely used in fields like physics, chemistry, and engineering when dealing with data that spans multiple orders of magnitude, such as sound levels or pH values.

    Example:

    $$[
    \log 100 = 2 \quad \text{because} \quad 10^2 = 100
    ]$$

    Most calculators use base 10 by default when you press the log button. This makes common logs particularly useful for quick manual calculations.

    1. Natural Logarithm (Base e)

    This type of logarithm uses Euler’s number (e ≈ 2.718) as the base and is written as ln x. It’s especially important in higher mathematics, particularly calculus, due to its natural properties when dealing with rates of change, exponential growth, or decay.

    Example:

    • lne=1

    You’ll often see natural logarithms used in population growth models, radioactive decay, and compound interest calculations, where continuous growth is involved.

    1. Binary Logarithm (Base 2)

    The binary logarithm, written as log , is crucial in computer science. Since digital systems operate using binary (0s and 1s), this type of log helps analyze algorithms, data storage, and computational complexity.

    Example:$$[
    \log_{2} 8 = 3 \quad \text{because} \quad 2^3 = 8
    ]$$

    This form of logarithm is commonly used when calculating time or space efficiency in coding and algorithm design.

    Logarithm Rules and Properties

    To work with logarithms efficiently, it’s important to master a few fundamental rules. These logarithm rules allow you to simplify complex expressions, solve equations, and switch between different forms with ease. Whether you’re solving homework problems or using a log calculator, these properties are essential tools in your math toolkit.

    Product Rule

    Formula: $$[
    \log_{a}(xy) = \log_{a}(x) + \log_{a}(y)
    ]$$

    Example: $$[
    \log_{3}(9 \times 27) = \log_{3}(9) + \log_{3}(27) = 2 + 3 = 5
    ]$$

    .

    Quotient Rule

    Formula: $$[
    \log_{a}\left(\frac{x}{y}\right) = \log_{a}(x) – \log_{a}(y)
    ]$$

    Example: $$[
    \log_{2}\left(\frac{16}{4}\right) = \log_{2}(16) – \log_{2}(4) = 4 – 2 = 2
    ]$$

    Power Rule

    Formula: $$[
    \log_{a}(x^n) = n \cdot \log_{a}(x)
    ]$$

    Example: $$[
    \log_{5}(25^3) = 3 \cdot \log_{5}(25) = 3 \cdot 2 = 6
    ]$$

    Change of Base Rule

    Formula: $$[
    \log_{a}(b) = \frac{\log(b)}{\log(a)}
    ]$$

    Why Useful: Lets you calculate logs of any base using a standard log calculator.

    How to Use a Log Calculator

    Step-by-Step Guide

    • Step 1: Identify the Base: Most calculators default to base $$ [\log_{a}(b) = \frac{\log_{10}(b)}{\log_{10}(a)}]$$
    • Step 2: Enter the Number: Type the value you want to find the log of.
    • Step 3: Switch Bases (if needed): Use the change of base rule for non-standard bases.

    Logarithm Formulas You Must Know

    To solve logarithmic expressions quickly and accurately, it’s essential to remember a few key formulas. These core rules simplify calculations, help solve equations, and are frequently used in algebra, calculus, and real-world applications. Think of them as your go-to shortcuts when working with logarithms—whether by hand or using a log calculator.

    FormulaExampleUse Case
    $$[
    \log_{a}(1) = 0
    ]$$    		$$[
    \log_{7}(1) = 0
    ]$$    		Simplifying equations
    $$[
    \log_{a}(a) = 1
    ]$$    		$$[
    \log_{5}(5) = 1
    ]$$    		Validating solutions
    $$[
    a^{\log_{a}(x)} = x
    ]$$    		$$[
    10^{\log(100)} = 100
    ]$$    		Solving exponential equations

    Solving Logarithmic Equations (with Examples)

    • Problem: Solve $$[\log_{4}(x) = 3]$$

    Solution: Convert to exponential form: $$[
    4^{3} = x \quad \rightarrow \quad x = 64
    ]$$

    .

    • Problem: Solve $$[2 \times \log_{3}(x) = 6]$$

    Solution: Divide by $$[
    2 \quad \rightarrow \quad \log_{3}(x) = 3 \quad \rightarrow \quad x = 3^{3} = 27
    ]$$

    Real-Life Applications of Logarithms

    1. Science: pH scale (logarithmic measure of acidity).

    2. Finance: Calculating compound interest.

    3. Engineering: Decibel levels for sound intensity.

    History of Logarithms

    Logarithms were invented by Scottish mathematician John Napier in 1614 as a way to simplify complex calculations. Before calculators existed, multiplying large numbers was time-consuming and error-prone. Napier’s logarithmic tables turned multiplication into simple addition, making calculations faster and more accurate.

    This breakthrough revolutionized fields like astronomy, navigation, and engineering, where precision and speed were critical. Later, Henry Briggs refined the concept by introducing common logarithms (base 10), which made the method even more practical and widely used.

    The invention of logarithms marked a turning point in mathematical history, laying the groundwork for modern computation long before electronic calculators.

    Common Errors and Misconceptions

    • Mistake: Assuming $$[\log(a b) = \log(a) + \log(b)]$$

    Truth: Only works for products $$(log(ab) = log(a) + log(b))$$.

    • Mistake: Ignoring domain restrictions $$(log(0) or log(-1)$$ are undefined).

     Final Thoughts: Why Learn Logarithms?

    So, why learn logarithms? Because they unlock deep mathematical understanding and have real applications in science, finance, and tech. They’re also critical for higher-level studies, including algebra, calculus, and data science.

    With the help of a log calculator, learning and applying logs becomes less intimidating and more accessible. Whether you’re solving equations, interpreting data, or preparing for exams, mastering logarithms gives you an edge.

    Now that you know what a logarithm is, how about practicing a few examples using your favorite calculator tool? You might just find logarithms more interesting than you expected.

  • What is Rounding? A Beginner’s Guide with Examples

    What is Rounding? A Beginner’s Guide with Examples

    Do long decimals or uneven numbers leave you puzzled? Whether you’re calculating money, estimating time, or analyzing data, rounding numbers makes your math simpler and your life easier. But what is rounding, and how do we actually do it?

    In this beginner-friendly guide, you’ll learn the definition of rounding numbers, why we do it, the different methods involved, and how to round whole and decimal numbers correctly. You’ll also find real-life examples and discover how to use a rounding numbers calculator for quick results.

    Let’s break it all down, step-by-step.

    What Does It Mean to Round a Number?

    Rounding means adjusting a number to make it simpler or more manageable while keeping it close to the original value. The goal is not to change the number drastically but to approximate it to a nearby value that’s easier to work with.

    For example:

    • 62 rounded to the nearest ten is 60
    • 3.146 rounded to the nearest hundredth is 3.15

    So, when someone asks, “what do you mean by rounding off a number?”, the answer is: it’s a method of simplifying numbers for easier estimation or calculation.

    Why Do We Round Numbers?

    We round numbers all the time—without even thinking about it. Think about shopping, distance estimation, or even telling the time.

    Here are some common reasons:

    • Money: Estimating $4.97 as $5
    • Time: Saying 3:58 PM is “about 4 PM”
    • Distance: Saying 1.9 miles is “about 2 miles”

    The purpose of rounding numbers is to simplify. It helps when exact values aren’t needed or are hard to work with. Rounding in math in real life saves time and makes communication smoother.

    Rules for Rounding Numbers

    To round numbers correctly, follow the standard rules:

    1. Identify the digit to round to (tens, hundreds, tenths, etc.)
    2. Look at the digit right after it
    3. If that digit is 5 or higher, round up
    4. If it is 4 or lower, round down

    For example:

    • 84 → Nearest ten → 80 (since 4 is less than 5)
    • 86 → Nearest ten → 90 (since 6 is greater than 5)

    These are the basic rules for rounding numbers and apply whether you’re dealing with decimals, whole numbers, or significant figures.

    How to Round Numbers (Step-by-Step)

    Step 1: Decide which place you want to round to (e.g., tens, hundredths).

    Step 2: Look at the digit immediately to the right.

    Step 3: Apply the 5-and-up rule.

    Let’s try rounding 348 to the nearest hundred:

    • Look at the tens digit (4).
    • Since 4 is less than 5, round down.
    • Final answer: 300

    If you’re unsure, use a round numbers calculator or visualize it with a number line.

    Rounding Numbers on a Number Line

    A number line helps you see how close a number is to its rounded value.

    Example:
    To round 47 to the nearest ten, place it between 40 and 50.
    Since 47 is closer to 50, we round it up.

    Use this method to teach students rounding numbers with a number line—a great visual tool for beginners.

    Rounding Whole Numbers

    To the Nearest Ten

    Round 86 → nearest ten?
    Look at the digit in the ones place: 6 → round up.
    Final Answer: 90

    Try it yourself or check using a round numbers calculator.

    To the Nearest Hundred

    Round 348 → nearest hundred?
    Tens digit = 4 → round down.
    Final Answer: 300

    To the Nearest Thousand

    Round 8,472 → nearest thousand?
    Hundreds digit = 4 → round down.
    Final Answer: 8,000

    Use these examples to practice rounding whole numbers for budgeting, taxes, or large estimations.

    Rounding Decimal Numbers

    Decimals can be tricky, but the same rules apply.

    To the Nearest Whole Number

    Round 3.6 → nearest whole number?
    Tenth digit = 6 → round up → 4

    To the Nearest Tenth

    Round 3.76 → nearest tenth?
    Hundredth digit = 6 → round up → 3.8

    To the Nearest Hundredth

    Round 3.746 → nearest hundredth?
    Thousandth digit = 6 → round up → 3.75

    Understanding how to round decimal numbers is important for scientific work, cooking, or dealing with currency.

    Rounding to Significant Figures

    Significant figures are used in science, finance, and engineering to express precision.

    What are they?

    They’re the digits that carry meaning. For example:
    0.0165 has 3 significant figures (1, 6, 5).

    How to Round to Sig Figs

    Round 0.0165 to 2 significant figures → 0.017

    These rules help avoid over-complicating results. Try it using a significant figures calculator if needed.

    How to Round Numbers in Excel

    Spreadsheets often round numbers automatically or allow manual control.

    ROUND()

    =ROUND(A1, 2) → rounds to 2 decimal places

    ROUNDDOWN()

    =ROUNDDOWN(A1, 1) → always rounds down

    ROUNDUP()

    =ROUNDUP(A1, 0) → always rounds up

    These Excel formulas help with financial data or sales reporting. Many users ask, “why is Excel rounding my numbers?” This is usually due to format settings or formula behavior.

    Round Whole Numbers in Excel

    Use =ROUND(A1, 0) to round to the nearest whole number.

    Round Decimal Numbers in Excel

    Use =ROUND(A1, 2) to get two decimal places.

    Round Up / Down in Excel

    Use =ROUNDUP() and =ROUNDDOWN() to control direction.

    Having trouble? Try tutorials or test it using sample spreadsheets with the excel round numbers function.

    How to Round Numbers in Google Sheets, Python, JavaScript

    Google Sheets

    Same as Excel. Use =ROUND() formula.

    Python

    python

    CopyEdit

    round(3.146, 2)  # Output: 3.15

    JavaScript

    js

    CopyEdit

    Math.round(3.146 * 100) / 100; // Output: 3.15

    Knowing how to round numbers in Python or JavaScript is useful for data scientists, developers, or students in tech.

    Rounding Numbers Examples

    Let’s try some:

    1. Round 47 → Nearest 10 → 50
    2. Round 3.146 → Nearest hundredth → 3.15
    3. Round 0.0165 → 2 significant figures → 0.017
    4. Round 86 → Nearest 100 → 100

    These rounded numbers examples show how flexible and useful rounding can be.

    Interactive Rounding Numbers Calculator

    Tired of doing the math manually? Try our rounding numbers calculator to get instant answers. Whether you’re rounding decimals, whole numbers, or significant digits, the tool does it all.

    It also doubles as a round up numbers calculator, so you can specify the direction.

    Practice Questions on Rounding Numbers

    Let’s test your skills.

    1. Round 76 to the nearest 10
    2. Round 3.679 to the nearest hundredth
    3. Round 0.02947 to 3 significant figures
    4. Round 986 to the nearest hundred
    5. Round 5.4 to the nearest whole number

    Check answers using our rounding numbers worksheets or the calculator.

    Common Mistakes When Rounding

    Watch out for these:

    • Rounding 5 down (remember: 5 always rounds up)
    • Rounding the wrong digit
    • Forgetting place values
    • Using Excel without adjusting decimal places

    If you ask, “why is Google Sheets rounding my numbers?”, it’s often a formatting issue.

    FAQs on Rounding Numbers

    What is Rounding in Math?

    It’s a way to simplify numbers by adjusting them to a nearby value, like 47 becoming 50.

    What Are the Rules for Rounding?

    Use the 5-and-up rule:

    • 5 and above → round up
    • 4 and below → round down

    What is 62 Rounded to the Nearest Ten?

    Answer: 60

    Where Do We Use Rounding in Real Life?

    • Budgeting
    • Distance approximation
    • Estimating time
    • Cooking
    • Business analytics

    How to Round to the Nearest Tenth?

    Look at the hundredth digit:

    • If 5 or more → round up
    • Else → round down

    Example: 3.76 → 3.8

    Why Do We Round Numbers?

    To make numbers simpler for estimation, calculation, and communication.

    What Are Significant Digits in Rounding?

    They represent meaningful numbers in precision contexts like science or measurements.

    Conclusion: Rounding Makes Life Easier

    Rounding is one of the most useful tools in everyday math. It helps simplify calculations, reduce error, and communicate results effectively. Whether you’re learning math basics or working with financial reports, understanding how to round numbers accurately is essential.

    Want instant answers? Use our rounding numbers calculator and practice with worksheets to master the skill.

  • Base and Power: What They Mean in Exponential Formulas

    Base and Power: What They Mean in Exponential Formulas

    Exponential formulas are at the heart of mathematics, science, and technology. Whether you’re calculating compound interest, modeling population growth, or understanding scientific notation, you’ll frequently encounter base and power in exponential formulas. These two components—base and power—form the foundation of exponential expressions.

    In this guide, we’ll explore what base and power mean, how they work together, common mistakes to avoid, and how they appear in real-world applications. Whether you’re a student, teacher, or curious learner, this deep dive will help you grasp exponent concepts clearly and confidently.

    What Is a Base in an Exponential Expression?

    In any exponential formula, the base is the number that gets multiplied repeatedly. It’s the starting point—the foundation on which powers act. In the expression $$232^{323}$$, the number 2 is the base. It tells us what number to multiply.

    Understanding the base in exponent form is crucial because it determines the scale of the result. A base of 10 grows faster than a base of 2 when raised to the same power.

    Examples of Common Bases

    Some commonly used bases include:

    • Base 2: Used in computing and binary systems.
    • Base 10: The standard in everyday arithmetic and scientific notation.
    • Base e (~2.718): Essential in calculus and natural exponential growth.

    These examples of base numbers appear in everything from financial modeling to programming.

    Visualizing the Base

    To help visualize how a base works, imagine a number tree: start with the base at the root and multiply it by itself as many times as the exponent says. For example, $$81 = 3 \times 3 \times 3 \times 3 = 3^4 = 81$$

    Base visuals and exponent diagrams are powerful learning tools. They show how the base repeats itself through multiplication, helping learners better understand the logic behind exponential formulas.

    Why the Base Matters

    Even a small change in the base can cause a significant shift in results. For instance:

    $$25 = 3^{2} \times 2^{5}$$

    $$35 = 24 \times 3 \times 3^5 = 24335 = 243$$

    This illustrates the importance of base value in exponential growth. Understanding the role of the base helps you predict outcomes and model real-world phenomena more accurately.

    What Does the Power Represent?

    If the base is the foundation, the power (or exponent) is the instruction—it tells us how many times to multiply the base by itself. In $$535^{353}$$, the power is 3, which means multiply 5 three times:$$5 \times 5 \times 5 = 125$$

    The power in exponential formulas controls the intensity of the multiplication. Larger powers lead to faster growth, and understanding this dynamic is crucial when solving exponent problems.

    Positive Powers

    Positive powers are the most common. They represent straightforward multiplication:

    $$8^3 = 8 \times 8 \times 8 = 512$$

    $$16^2 = 16 \times 16 = 256$$

    $$10^5 = 100,000$$

    These are clear examples of positive powers in action. They also show how quickly numbers grow when raised to higher powers.

    Zero and One as Powers

    Special exponent rules come into play with zero and one:

    • Anything raised to the power of 1 stays the same: $$7^1 = 7$$
    • Anything to the power of 0 equals 1: $$990=199^0 = 1$$

    These exponent rules for 0 and 1 are critical to remember. They’re consistent across all math levels and serve as shortcuts in calculations.

    Negative Powers

    What does a negative exponent mean? A negative power indicates a reciprocal:

    $$2^{-3} = \frac{1}{2^{3}} = \frac{1}{8}$$

    This rule shows that negative exponents flip the base. Negative power examples appear frequently in algebra and scientific formulas.

    Relationship Between Base and Power

    The interaction between base and power determines the result of an exponential expression. Think of it as a team effort—while the base sets the number, the power decides the magnitude.

    For example:

    $$24 = 16 \times 2 \times 4$$

    $$4^{2} = 16$$

    Both result in the same value but are structurally different. The base-power relationship plays a key role in algebra, physics, and computer science.

    Differences Between Exponential, Radical, and Linear Terms

    Exponential formulas differ from other expressions in how they grow:

    • Exponential: Involves multiplication and rapid growth (e.g., $$2n \times 2^n \times 2n$$
    • Radical: Involves roots (e.g., $$x \sqrt{x}$$
    • Linear: Involves constant rate of change (e.g., y=mx +by = mx + by=mx +b)

    Understanding exponential vs radical vs linear helps distinguish between types of equations and their behaviors. Exponential growth, in particular, accelerates far more quickly.

    Common Mistakes When Interpreting Base and Power

    Even advanced learners make mistakes with exponents. Let’s address the most frequent ones.

    Misinterpreting $$(-2)^4 = 16$$

    This is a classic pitfall. The parentheses make all the difference:

    $$(-2)^4 = 16$$

    $$-2^4 = -16$$

    Without parentheses, only the 2 is raised, and the negative sign applies afterward. Always consider order of operations and how parentheses affect the base and power in exponential formulas.

    Forgetting Rules of Zero Power

    Many forget that any non-zero number raised to the 0 power equals 1. That includes decimals, fractions, and negatives:

    $$(-5)^0 = 1$$

    $$\left(\frac{1}{2}\right)^0 = 1$$

    Remember this zero exponent truth to avoid common errors.

    How to Use an Exponent Calculator

    An Exponent Calculator helps you quickly solve exponent problems without doing the math by hand. Here’s how to use it:

    • Step 1: Enter the base (e.g., 4).
    • Step 2: Enter the power or exponent (e.g., 3).
    • Step 3: Click “Calculate” to get the result.

    Example: If your base is 4 and your exponent is 3, the calculator shows:

    • 4³ = 4 × 4 × 4 = 64

    It’s perfect for checking homework, solving complex expressions, or learning how exponents work.

    Save time and avoid mistakes with a reliable Exponent Calculator.

    Base and Power in Real-World Applications

    Exponential formulas aren’t just academic—they’re everywhere. You’ll find base and power in physics, chemistry, economics, and everyday tech.

    Scientific Notation and Base 10

    Scientific notation helps represent very large or small numbers compactly:

    $$11.23 \times 10^{6} = 1,230,000$$

    The base 10 is constant, and the power tells us how many places to move the decimal. This is widely used in science, engineering, and data storage.

    Binary in Computing (Base 2)

    Computers rely on binary, or base 2, to represent data. Every bit is a power of 2:

    $$2^0 = 1, \quad 2^1 = 2, \quad 2^2 = 4$$

    Understanding binary exponent use is essential for careers in programming, cybersecurity, and digital systems.

    Exponential Growth Models (Base > 1)

    Real-world exponential growth examples include:

    • Population increase: $$P = P_0 (1 + r)^t$$
    • Compound interest: $$A = P \left(1 + \frac{r}{n}\right)^{nt}$$
    • Virus spread: Doubling rates over time

    In each case, the base represents the growth rate, and the power reflects the time or repetitions. These base power growth models help forecast future scenarios.

    Interactive Base and Power Quiz

    Want to test your knowledge? Try these quick questions:

    1. What is $$323^{232}$$
    2. Simplify $$505^{050}$$
    3. True or False: $$(-4)^2 = -16$$
    4. What does a negative exponent mean?
    5. Which grows faster: linear or exponential?

    These exponent MCQs reinforce key learning points and provide helpful review.

    Printable Reference Table: Base & Power Rules

    Here’s a handy chart you can print or save:

    ExpressionBasePowerResult
    $$232^{323}$$238
    $$10010^{0}100$$1001
    $$(3)^1$$313
    $$5 – 2^{-2}$$5-21/25
    $$xnx^nxn$$xnxⁿ

    This exponent cheat sheet is great for quick reference when solving math problems.

    Understanding base and power in exponential formulas opens the door to a wide range of math and science applications. From solving equations to analyzing data growth, these two components work hand-in-hand to simplify complex ideas and power our digital world.

    Whether you’re learning exponents for the first time or brushing up for an exam, always remember:

    • The base is what you multiply.
    • The power tells how often.

    Together, they form the building blocks of exponential logic.

    Frequently Asked Questions (FAQs)

    What is the difference between base and power?

    The base is the number being multiplied. The power tells how many times to multiply it. For example, in 434^343, 4 is the base and 3 is the power.

    Can the base be a variable like x?

    Yes! Algebra often uses variables as bases. Examples include:

    $$x^2a^{b}x^n$$

    These are common in equations and functions.

    Is power always a whole number?

    No. Powers can be:

    • Negative: $$3^{-2} = \frac{1}{3^2} = \frac{1}{9}$$
    • Fractional: $$9^{\frac{1}{2}} = \sqrt{9} = 3$$
    • Decimal: $$100^{0.5} \approx 3.16$$

    These are known as non-integer exponents.

    What is the base in scientific notation?

    It’s always 10. Scientific notation expresses numbers as a decimal multiplied by a power of 10:

    $$2.5 \times 10^3 = 2,500$$

    Why does anything to the power of 0 equal 1?

    Mathematically, it’s defined that way. When you reduce exponents step-by-step, anything⁰ equals 1 by logical progression. It’s a foundational math rule.

    How do parentheses affect base and exponent?

    Parentheses change the scope of what’s raised. Compare:

    $$(-3)^2 = 9$$

    $$-3^2 = -9$$

    This difference is key to proper exponent notation.

    Can both base and exponent be variables?

    Yes. Advanced math often uses expressions like:

    $$xyx^yxy$$

    $$aba^bab$$

    These appear in calculus, statistics, and computer science.

  • Understanding Binary Logic Gates and Their Applications

    Every time you use a calculator, unlock your phone, or run a computer program, you’re relying on binary logic gates and their applications – the silent powerhouses of the digital world. These tiny electronic circuits form the foundation of all modern electronics.

    In this comprehensive guide, we’ll explain what binary logic gates are, how they work, the different types, and where they’re used in real-life technology. Whether you’re a beginner or brushing up on digital basics, this article will simplify understanding logic gates and their importance in today’s computing landscape.

    Introduction to Logic Gates

    Logic gates are the building blocks of digital electronics. These are tiny electronic circuits that perform logical decisions using binary inputs (0 and 1). They follow Boolean algebra to produce specific outputs based on input combinations.

    In digital systems, every task—no matter how complex—boils down to combinations of logic gate operations. That’s why binary logic gates are found in every computer chip, smartphone, washing machine, and smart home device.

    What Are Binary Logic Gates?

    Binary logic gates are electronic devices that process binary inputs to produce binary outputs. These outputs depend on predefined logical operations, like AND, OR, and NOT.

    Each logic gate takes one or more binary inputs and returns a binary result—either 1 (true) or 0 (false). This enables computers and digital circuits to make decisions, execute instructions, and control operations.

    For example:

    • The AND gate returns 1 only if both inputs are 1.
    • The OR gate returns 1 if at least one input is 1.
    • The NOT gate flips the input.

    These fundamental gates help create circuits that control everything from your alarm clock to your car engine.

    Types of Binary Logic Gates

    There are two main categories of logic gates: basic gates and compound or advanced gates. Understanding these types helps in grasping how digital circuits work at the hardware level.

    Basic Logic Gates

    The three primary gates are:

    1. AND Gate
      • Output is 1 only when all inputs are 1.
      • Example: 1 AND 1 = 1, but 1 AND 0 = 0
    2. OR Gate
      • Output is 1 if at least one input is 1.
      • Example: 1 OR 0 = 1, 0 OR 0 = 0
    3. NOT Gate
      • Inverts the input.
      • Example: NOT 1 = 0

    These are the basic logic gates found in most digital devices. They form the core of binary logic operations.

    Universal Logic Gates: NAND and NOR

    1. NAND (NOT + AND)
      • Output is 0 only when all inputs are 1.
      • It’s the inverse of the AND gate.
    2. NOR (NOT + OR)
      • Output is 1 only when all inputs are 0.
      • It’s the inverse of the OR gate.

    These are called universal logic gates because they can be combined to replicate any other gate. They’re widely used in circuit design, especially in microchips and embedded systems.

    Exclusive Logic Gates: XOR and XNOR

    1. XOR (Exclusive OR)
      • Output is 1 only when inputs are different.
      • Great for bit comparison and parity checks.
    2. XNOR (Exclusive NOR)
      • Output is 1 when inputs are the same.
      • Useful in equality testing and arithmetic circuits.

    These exclusive logic gates are vital for adder circuits, encryption, and error detection in communication systems.

    Truth Tables and Logic Symbols

    To understand how logic gates work, we use truth tables—a structured way of showing all possible input and output combinations.

    Example: AND Gate Truth Table

    ABOutput (A AND B)
    000
    010
    100
    111

    Each logic gate also has a symbol used in circuit diagrams. These symbols help electronics engineers and students visualize how circuits are designed.

    Applications of Logic Gates

    Now let’s explore logic gate applications in real-life. You’ll be surprised how often these gates are at work behind the scenes in your everyday gadgets.

    Logic Gates in Computers and Processors

    Modern CPUs and memory units are made entirely of logic gates. They control:

    • Arithmetic Logic Units (ALUs) for math operations
    • Registers for short-term memory
    • Control units for instruction execution

    Every function in a computer—opening a file, saving a document, loading a webpage—is powered by binary logic gates executing instructions in nanoseconds.

    Logic Gates in Everyday Devices

    From digital watches to microwave ovens, logic gates in devices help manage simple on/off decisions.

    Examples:

    • Remote Controls: Use logic gates to encode and decode IR signals.
    • Washing Machines: Control water levels, timers, and cycles using gate-based control logic.
    • Toys: Interactive features respond based on binary inputs.

    Logic gates in everyday electronics are what make automated decisions possible.

    Logic Gates in AI and Robotics

    AI chips and robot controllers use complex logic circuits to make decisions in real time. These include:

    • Sensors that convert physical data to binary
    • Processors that use XOR and AND gates for conditional logic
    • Feedback loops using XNOR gates for pattern matching

    Logic gates support the rapid decision-making processes in autonomous drones, smart assistants, and self-driving vehicles.

    Designing Circuits with Logic Gates

    Engineers and hobbyists design digital systems by combining logic gates into larger circuits that perform specific functions.

    Example Projects:

    • Half Adder/Full Adder: Adds two binary numbers
    • Multiplexers: Select between multiple inputs
    • Flip-Flops: Store a single bit of data

    Designers use schematics and simulation tools to test how inputs behave across different gate combinations. Tools like Multisim, Tinker cad, or physical breadboards help in learning how to design logic circuits.

    Binary Calculator for Logic Gates

    Want to see how logic gates work in real time? A Binary Calculator lets you apply logic operations like AND, OR, and XOR to binary numbers instantly.

    Example:

    • A = 1010, B = 1100
    • A AND B = 1000
    • A OR B = 1110

    It’s a simple way to test binary inputs and understand gate behavior—perfect for students, hobbyists, or quick checks during circuit design.

    Why Binary Logic Gates Matter

    Binary logic gates are the core of all digital technology. From simple sensors to quantum processors, logic gates provide the binary framework needed for decision-making, automation, and computing.

    They allow devices to:

    • Make binary decisions
    • Store and process data
    • Execute commands
    • Interface with the real world

    Without them, our digital age simply wouldn’t exist. So, understanding logic gates is not just about circuits—it’s about the digital logic that powers your everyday life.

    FAQs

    What is a binary logic gate?

    It’s an electronic circuit that takes binary inputs (0 or 1) and produces a binary output based on a logical operation (e.g., AND, OR, NOT).

    Why are NAND and NOR called universal gates?

    Because you can combine NAND or NOR gates to create any other logic gate, including AND, OR, and NOT. They are extremely versatile and form the basis of digital circuit design.

    What do truth tables show?

    Truth tables list all possible input combinations for a logic gate and their corresponding outputs. They help in predicting circuit behavior.

    Where are logic gates used in real life?

    Logic gates are everywhere—in calculators, alarms, traffic lights, appliances, smartphones, and even children’s toys. They’re used in both complex systems and simple circuits.

    How do logic gates relate to binary numbers?

    Logic gates operate on binary values—0 and 1. These gates take binary inputs, apply logic, and return binary outputs. That’s why they’re crucial in digital logic circuits.

    Can I build circuits with logic gates at home?

    Yes! You can use:

    • Breadboards and ICs (Integrated Circuits)
    • Online simulators like Tinkercad
    • Arduino or Raspberry Pi kits

    These are great for students and hobbyists learning electronics.

    Are logic gates still relevant in modern computers?

    Absolutely. While today’s chips are extremely advanced, they are still made up of millions (or billions) of logic gates. They’re essential to CPU design, memory control, and AI chip functionality.

  • How to Calculate Percent of a Given Value

    How to Calculate Percent of a Given Value

    Have you ever wondered how to calculate percent of a given value quickly and accurately? Whether you’re splitting a restaurant bill, calculating exam scores, or working out discounts, knowing how to find the percent of a value is a skill you use almost every day. This step-by-step guide will walk you through everything from the basic percentage formula to real-life applications and even how to calculate percentage when the total isn’t 100. 

    We’ll also explore how to reverse-engineer percentages, solve common word problems, and even learn how to use an online percentage calculator. Imagine being able to calculate the percentage of marks, find what percent of X is Y, or convert percentages to decimals and fractions without hesitation. Understanding the meaning of percentage and its real-world uses can make daily tasks—from shopping to budgeting—much simpler and smarter.

    Read on to discover how to calculate percent step by step. By the end, you’ll not only master the percentage formula but also feel confident applying it in any situation—be it exams, shopping, or business reports. Let’s get started and make percentage calculation easy and clear!

    What is a Percentage?

    A percentage is a way to express a part of a whole as a fraction of 100. In math, “percent” literally means “per hundred.” For example, 50% simply means 50 out of 100.

    Meaning of percentage becomes clear when we look at daily life: calculating discounts, measuring growth, or even scoring marks in an exam. Knowing what percentage in math helps us compare, measure, and understand numbers easily.

    Percentage examples:

    • Scoring 80% on a test means you got 80 out of 100.
    • A store offering 25% off means you pay 75% of the original price.

    Understanding the percent meaning is the first step to confidently calculating and using percentages every day.

    Understanding Percentage

    To understand percentage better, think of it as a tool to simplify comparisons. It doesn’t matter how big or small the actual numbers are—percentages make everything relative to 100.

    Basics of percent help us see how one number relates to another. For example:

    • 20 out of 40 is 50% (because 20 ÷ 40 × 100 = 50%).
    • 5 out of 25 is 20%.

    Visual aids, like pie charts or bars, also make it easier to understand percent and spot trends quickly.

    Common Uses of Percentages in Real Life

    Percentages in daily life are everywhere:

    • Shopping discounts: 30% off means you pay 70% of the price.
    • Taxes: VAT of 13% adds 13% to your bill.
    • Grades: 85% score shows your performance.
    • Business: Profit margin, commission, and market share are all in percentages.
    • Statistics: Surveys often show data in percent for easy comparison.

    These real-life percentage examples show why learning to calculate percent is so useful.

    Percentage Formula

    The core percentage formula is simple:

    • Percentage (P) = $$\left( \frac{\text{Part} \ (X)}{\text{Whole} \ (Y)} \right) \times 100$$

    Where:

    • X = part or value
    • Y = total or whole

    This percentage calculation formula helps you find what part of the total a number represents. Whether it’s exam marks, sales numbers, or survey results, this formula to calculate percentage always applies.

    Example: If you scored 45 marks out of 60, your percentage is:

    • $$\left( \frac{45}{60} \right) \times 100 = 75\%$$

    How to Calculate Percentage of a Number

    Here’s a step-by-step guide on how to calculate percentage of a number:

    1. Decide the percent you need to find (P).
    2. Multiply that percent by the number (N).
    3. Divide by 100.

    Example: Find 20% of 150.

    • (20×150)÷100=30

    This method helps you easily find the percent of a value in any situation.

    How to Calculate Percentage When Total Is Not 100

    Sometimes, the total number isn’t 100. Don’t worry—the same method works:

    • Percentage = $$\left( \frac{\text{Part}}{\text{Total}} \right) \times 100$$

    Example:

    Out of 250 people, 125 voted yes:

    • (125÷250)×100=50%

    This shows how to calculate the percentage when the total differs from 100.

    How to Calculate X If Y Is P Percent of X

    This is called reverse percentage calculation:

    1. You know Y (part) and P% (percent).
    2. Use formula:

    $$X = \frac{Y \times 100}{P}$$

    Example:

    30 is 20% of what number?

    • (30×100)÷20=150

    You’ve found the original number.

    Calculate P Percent of What Is Y

    Want to find the total when you know the part and percent?

    Use the same reverse formula:

    • $$\text{Total} = \frac{\text{Part} \times 100}{\text{Percent}}$$

    Example:

    15 is 10% of what?

    • (15×100)÷10=150

    What Percent of X is Y?

    To find what percent one number is of another:

    • $$\left( \frac{Y}{X} \right) \times 100$$ 

    Example:

    What percent of 80 is 20?

    • (20÷80)×100=25%

    This helps compare values easily.

    Percent given value Calculator

    For quick answers, use a free online percent given value calculator. Just enter the numbers, and it instantly shows the result. This tool saves time when you need to calculate percentages online.

    How to Calculate Percentage Change

    Percentage change formula:

    $$\left( \frac{\text{New Value} – \text{Old Value}}{\text{Old Value}} \right) \times 100$$

    • Positive result: percent increase
    • Negative result: percent decrease

    Example:

    Price increased from $50 to $60:

    • (60−50)÷50×100=20%

    Percentage Increase and Decrease

    Use these formulas:

    • Increase:

    $$\left( \frac{\text{Increase}}{\text{Original Value}} \right) \times 100$$

    • Decrease:

    $$\left( \frac{\text{Decrease}}{\text{Original Value}} \right) \times 100$$

    They help track price changes, growth, or loss.

    How to Calculate Percentage of a Number

    Calculating the percentage of a number is a fundamental skill useful in everyday life—from finding discounts to analyzing data. Here’s a step-by-step guide on how to find percent of value easily.

    Step 1: Understand the Percent Formula

    To calculate percent of a number, use the simple formula:

    • Percentage=(Part÷Whole)×100

    But when you want to find what is X% of a number (let’s say number = N), the formula becomes:

    • X% of N=(X÷100)×N

    This formula is the backbone of every percentage calculation.

    Step 2: Apply the Formula with Examples

    Let’s see how this works in practice.

    Example 1: Find 20% of 150

    • 20% of 150=(20÷100)×150=0.2×150=30

    So, 20% of 150 is 30.

    Example 2: Find 35% of 80

    • 35% of 80=(35÷100)×80=0.35×80=28

    So, 35% of 80 is 28.

    These simple steps show exactly how to calculate the percentage of a number without confusion.

    Step 3: Use Percent in Real-Life Scenarios

    Percentages help with:

    • Calculating discounts during shopping (e.g., 15% off a price)
    • Working out tax or tip amounts
    • Analyzing data, scores, or test results

    Conversion Between Percentages, Decimals and Fractions

    Understanding how to convert between percentages, decimals, and fractions helps you move seamlessly between different ways of expressing the same value. Here’s a quick step-by-step guide:

    Percent to Decimal

    To convert a percent to a decimal, simply divide by 100 (or move the decimal point two places to the left).

    Example:

    • 25% → 25 ÷ 100 = 0.25

    This is useful when calculating percentages of numbers.

    Decimal to Percent

    To convert a decimal to a percent, multiply by 100 (or move the decimal point two places to the right).

    Example:

    • 0.75 × 100 = 75%

    Always add the percent sign (%) at the end.

    Percent to Fraction

    To turn a percent into a fraction, write it over 100 and then simplify.

    Example:

    • 50% → 50/100 → simplify → 1/2

    This method shows the relationship clearly and is especially useful in math and statistics.

    Fraction to Percent

    To convert a fraction to a percent, first divide the numerator by the denominator to get a decimal, then multiply by 100.

    Example:

    • 3/4 → 0.75 → 0.75 × 100 = 75%

    These conversions make it easy to switch forms depending on what’s clearer or more useful—whether you’re solving math problems, calculating discounts, or analyzing data.

    Showing Trends with Percentages

    Percentages aren’t just for single calculations—they’re powerful tools for spotting trends and patterns over time.

    By expressing data as percentages, you can easily compare values across different periods, sizes, or groups. For example:

    • Sales growth: Comparing this year’s sales to last year’s as a percentage increase or decrease.
    • Profit margins: Showing profit as a percentage of total revenue to track business health.
    • Survey results: Highlighting shifts in customer satisfaction or preferences.

    Using percentages in trend analysis makes complex data clearer and helps reveal underlying changes, making it easier to explain insights to others.

    Common Percentage Word Problems

    Understanding how to calculate percent helps solve many real-life questions—like discounts, comparisons, and changes over time. Practice makes perfect! Here are a few common types of percentage problems:

    • What is 15% of 200?
    • Use the formula: (15 × 200) ÷ 100 = 30
    • The price dropped from $80 to $60. What’s the percent decrease?

      $$\left( \frac{80 – 60}{80} \right) \times 100 = \left( \frac{20}{80} \right) \times 100 = 25\%$$
    • 45 is what percent of 90?
      $$\left( \frac{45}{90} \right) \times 100 = 50\%$$

    Solved Examples on Percentage

    Example 1:

    Find 25% of 120.

    • (25×120)÷100=30

    Example 2:

    What percent of 200 is 50?

    • (50÷200)×100=25%

    Example 3:

    The price increased from $150 to $180. What’s the percent increase?

    • (180−150)÷150×100=30÷150×100=20%

    Example 4:

    Find 12% of 250.

    • (12×250)÷100=30

    Practice Questions on Percentage

    Now it’s your turn! Try these:

    • Find 10% of 250.
    • What is 35% of 80?
    • 30 is what percent of 120?
    • Find 15% of 300.
    • The price dropped from $90 to $72. What is the percent decrease?
    • What percent of 400 is 50?
    • Increase 250 by 20%.
    • The test score increased from 60 to 75. Find the percentage increase.
    • Find 5% of 600.
    • 80 is what percent of 160?

    Practicing these helps build confidence in percentage calculation and makes it easier to tackle real-world problems.

    Bonus: Percentage Calculator Tool

    Need to double-check your answers or save time on tricky problems?

    Use our free online percentage calculator to quickly:

    • Find what percent one number is of another
    • Calculate a percentage of any number
    • Work out percentage increase or decrease

    This handy tool helps with everything from homework to shopping discounts—making percentage calculation faster and easier anytime you need it!

    Frequently Asked Questions (FAQs)

    What is the difference between percentage and percent?

    Both refer to parts per hundred. “Percent” comes after a number (e.g., 25 percent), while “percentage” is a general noun used to describe an amount or rate.

    What is a percentage?

    A percentage expresses a number as a fraction of 100. It helps compare proportions easily, like saying 50% means half.

    Can percentages be more than 100?

    Yes, they can. This happens when the part exceeds the whole, like a 120% increase or when profits double.

    What is the percentage of marks?

    It shows how many marks you scored out of the total possible marks, converted to percent. Use: (marks obtained ÷ total marks) × 100.

    What is the formula to convert a number into a percentage?

    Divide the part by the whole, then multiply by 100. For example: (25 ÷ 200) × 100 = 12.5%.

    How do I calculate a percentage of a number?

    Multiply the number by the percentage written as a decimal. Example: 20% of 150 → 0.20 × 150 = 30.

    How do I calculate what percentage one number is of another?

    Divide the first number by the second and multiply by 100. Example: (40 ÷ 200) × 100 = 20%.

    How do I calculate percentage increase or decrease?

    Subtract the old value from the new value, divide by the old value, and multiply by 100. Example: ((120−100) ÷ 100) × 100 = 20%.

    How do I calculate the percentage of marks?

    Same method: (marks obtained ÷ total marks) × 100. It’s the standard way to show your score as a percent.

    How do I calculate the total if I know the percentage and the part?

    Use the formula: total = part ÷ (percentage ÷ 100). For instance, if 40 is 25%, total = 40 ÷ 0.25 = 160.

    How to calculate a discount using percentage?

    Multiply the original price by the discount percent as decimal, then subtract from the price. Example: 15% of $200 → $30, final price = $200−$30=$170.

    How to calculate the percentage of money (tax, tip, interest)?

    Use: amount × rate (as decimal). Example: 8% tax on $50 → 0.08×50=$4.

    What is the Excel formula to calculate percentage?

    Type = (part/whole)100 in a cell. For example, if A1=25 and B1=200, =A1/B1100 shows 12.5%.

    How to calculate the percentage difference between two numbers?

    Find the difference, divide by the average of the numbers, then multiply by 100. Example: numbers 60 and 80 → difference=20; average=70; (20/70)×100≈28.6%.

    How can I quickly calculate percentages without a calculator?

    Estimate by rounding numbers. For 10%, move the decimal left once; for 5%, halve 10%; for 20%, double 10%.

    How to convert a decimal into a percentage?

    Multiply by 100 and add the % symbol. Example: 0.45×100=45%.

    How to convert a fraction into a percentage?

    Divide the numerator by the denominator, then multiply by 100. Example: 3/4 →0.75×100=75%.

    What is the difference between percentage increase and percentage change?

    Percentage increase refers only to growth, while percentage change can mean increase or decrease. Both use similar formulas but describe different situations.

    How to calculate what percent remains after a decrease?

    Subtract the percentage decrease from 100%. Example: after 20% decrease → 100−20=80% remains.

    Why do we use percentages?

    Percentages make comparing numbers simpler by standardizing values out of 100. They’re widely used in finance, science, statistics, and daily life.

  • What is Percent Error? Understand It with This Simple Calculator

    What is Percent Error? Understand It with This Simple Calculator

    Have you ever measured something and wondered, “How close am I to the real value?” Whether you’re a student solving physics problems, a scientist working in a lab, or a professional dealing with estimations, knowing how accurate your results are matters a lot. That’s where percent error becomes essential. 

    This simple yet powerful concept helps you compare your measured or estimated values against the actual, accepted values. And to make life easier, we’ve created a percent error calculator—a tool designed to simplify your work and boost accuracy in just a few clicks. Imagine instantly finding out whether your results are slightly off, perfectly on track, or wildly different. 

    With our calculator and clear guide, you’ll learn exactly how to calculate percent error, understand why it matters, and avoid common mistakes. Keep reading to explore the meaning of percent error, learn the formula, see real examples, and discover expert tips. Let’s get started!

    What is Percent Error?

    At its core, percent error is a measure that shows the difference between an estimated or measured value and the true or actual value, expressed as a percentage. In simple words, percent error tells you how wrong (or right) your measurement is when compared to the accepted standard. This makes it a critical concept in math, science, engineering, and even everyday calculations.

    People often ask, “What is percent error in math?” Think of it this way: if you predict something should weigh 105 grams, but it actually weighs 100 grams, a percent error helps you see the difference as a percentage. The meaning of percent error becomes clearer when you realize it’s not about blaming mistakes—it’s about understanding accuracy.

    Why Do We Calculate Percent Error?

    Calculating percent error helps us measure how close our estimates or experimental results are to the actual, accepted values. It’s a simple but powerful way to check accuracy, improve methods, and build confidence in data across science, engineering, and everyday problem-solving.

    • Evaluate Accuracy: In science, experiments rarely produce perfect results. Percent error helps us understand how close our measurements are to the real value.
    • Compare Methods: When using different techniques, calculating percent error shows which method is more reliable.
    • Educational Value: Teachers and students use percent error to check the quality of lab experiments and calculations.
    • Practical Use: Engineers and manufacturers use it to maintain product quality and reduce production flaws.

    By calculating percent error, you turn raw numbers into meaningful insights—helping you learn, improve, and avoid repeating the same mistakes.

    Percent Error Formula

    The standard percent error formula is simple yet powerful:

    Percent Error = $$\left| \frac{\text{Measured Value} – \text{Actual Value}}{\text{Actual Value}} \right| \times 100$$

    Where:

    • Measured Value: The value you found, estimated, or observed.
    • Actual Value: The accepted or true value.

    The absolute value signs ensure that percent error is usually expressed as a positive percentage (though it can sometimes be negative to show direction).

    1. How to Calculate Percent Error

    Here’s a quick, clear way to calculate percent error:

    1. Subtract Actual Value from Measured Value

    Example: Measured = 105, Actual = 100

    Difference = 105 – 100 = 5

    1. Take the Absolute Value

    Absolute difference = |5| = 5

    Divide by the Actual Value

    1. 5 ÷ 100 = 0.05

    Multiply by 100

    0.05 × 100 = 5%

    Your percent error is 5%.

    Note: Always check you’re using the actual value in the denominator. Many percent error calculation mistakes happen here!

    Absolute and Relative Error Explained

    Before understanding percent error fully, it helps to know what absolute and relative errors mean. These two concepts describe the size of measurement errors in different ways and together explain where percent error comes from.

    • Absolute Error: The difference between the measured value and the actual value (without considering direction).

    ∣Measured−Actual∣

    • Relative Error: Absolute error divided by the actual value (but before multiplying by 100).

               $$\frac{\text{Absolute Error}}{\text{Actual Value}}$$

    Percent error is simply the relative error multiplied by 100.

    Knowing these related terms helps deepen your understanding of measurement accuracy.

    Percent Error Calculation Examples

    Examples make learning easier by showing how the formula works in real situations. Let’s go through step-by-step percent error examples to see how to handle both positive and negative differences.

    Example 1: Positive Percent Error

    • Measured value: 110
    • Actual value: 100
    • Percent error:

                  $$\left( \frac{110 – 100}{100} \right) \times 100 = 10\%$$ 

    Example 2: Negative Percent Error

    Some prefer showing the direction:

    • Measured: 95
    • Actual: 100
    • (95 – 100) ÷ 100 × 100 = -5%

    Indicates the estimate was lower than the actual value.

    Example 3: Large Percent Error

    • Measured: 150
    • Actual: 100
    • Percent error:

    $$\left( \frac{50}{100} \right) \times 100 = 50\%$$

    How to Use the Percent Error Calculator

    Ready to simplify your work? Here’s a complete, step-by-step guide to using our percent error calculator effectively:

    Step 1: Gather Your Numbers

    Start by collecting two values:

    • Measured (or experimental) value: This is the number you got from your experiment, observation, or estimation.
    • Actual (or accepted) value: This is the true value recognized by experts, references, or known data.

    Double-check these numbers to make sure they’re accurate before entering them.

    Step 2: Enter the Measured Value

    • On the calculator page, you’ll see a field labeled “Measured Value” or “Your Result.”
    • Type in your measured value exactly as you recorded it. For example, if your measurement was 105 grams, enter 105.

    Step 3: Enter the Actual Value

    • Next, move to the field labeled “Actual Value” or “Accepted Value.”
    • Enter the standard or true value you’re comparing against. Using the same example, if the actual weight should be 100 grams, type 100.

    Always use the accepted value that’s widely recognized in textbooks, scientific tables, or standards.

    Step 4: Click ‘Calculate’

    After entering both values, press the Calculate button.

    The calculator instantly applies the formula:

           Percent Error = $$\left| \frac{\text{Measured} – \text{Actual}}{\text{Actual}} \right| \times 100$$

    Step 5: Read and Understand the Result

    • Your percent error result will appear on the screen—usually as a percentage like 5% or -5%.
    • Check if it’s positive, negative, or unusually large. A small percent error means your measurement was close to the actual value, while a larger percent error shows a bigger difference.

    Step 6: Troubleshoot if Needed

    If your result looks strange (e.g., unexpectedly high or negative when you didn’t intend it):

    • Check that you didn’t switch the measured and actual values.
    • Confirm that you used the correct actual value as the denominator.
    • Ensure your measured value is correct and typed in properly.

    Step 7: Reflect on Your Result

    Once you have your percent error, ask yourself what it means:

    • Is the error acceptable in your field or project?
    • Do you need to repeat your experiment to reduce error?

    By following these steps carefully, the percent error calculator becomes a powerful tool—not just for getting a quick answer, but for truly understanding your data and improving your accuracy.

    Experimental Value vs Theoretical Value

    In percent error calculations, you’ll often come across the terms experimental value and theoretical value—both of which play a key role in understanding accuracy.

    The experimental value is the number you obtain directly from your own experiment, observation, or measurement. It reflects real-world data that may include small variations or mistakes due to human error, instrument limitations, or environmental factors.

    On the other hand, the theoretical value—also called the accepted value—is the value recognized as correct by experts, research studies, or standard references. It’s usually based on repeated experiments, scientific theory, or published data that’s considered highly reliable.

    Percent error helps compare these two values by showing how far off your measurement is from the expected standard, expressed as a percentage. This makes it easier to judge the accuracy of your work, identify possible sources of error, and improve future experiments.

    Understanding the difference between experimental and theoretical values is essential for anyone learning about error analysis, whether in a science lab, engineering project, or daily calculation.

    What Is the Accepted Value in Percent Error?

    The accepted value is the true, standard, or reference value that scientists, engineers, or experts widely recognize as correct. It serves as the benchmark against which experimental results are compared.

    For example, the boiling point of pure water at sea level is 100°C, which is known through countless experiments and accepted by scientific consensus. When calculating percent error, you always use this accepted value in the denominator to see how close your measured result is to what’s generally considered accurate.

    Relying on the accepted value helps ensure your calculations are meaningful, consistent, and scientifically valid. It turns your raw data into an informed measure of accuracy.

    Margin of Error, Standard Error & Percent Error

    These three terms—percent error, standard error, and margin of error—may sound similar, but they have different meanings and uses in math and statistics.

    • Percent Error: Measures how far your single measured or experimental value is from the accepted or theoretical value, expressed as a percentage. It’s mainly used in science and measurement to check accuracy.
    • Standard Error: Describes the variability or spread of sample means around the actual population mean. It’s commonly used in statistics to understand how precise an estimated average is across multiple samples.
    • Margin of Error: Often used in polls and surveys, it shows the possible range your sample result could differ from the true population value, giving a sense of confidence in survey results.

    While each term helps quantify uncertainty, they apply in different contexts and calculations. Knowing which one to use helps you communicate your data more accurately and professionally.

    Mean Percentage Error vs Percent Error

    Understanding the difference between Mean Percentage Error (MPE) and percent error helps you choose the right approach depending on your data.

    • Percent Error is calculated from a single measurement by comparing it directly to the accepted value. It shows how far that one result is from what’s expected, making it useful for quick checks or individual experiments.
    • Mean Percentage Error (MPE), on the other hand, is the average of percent errors from multiple measurements or trials. It’s particularly useful when you want to evaluate the overall accuracy of a series of tests, repeated experiments, or a forecasting model.

    In summary, use percent error when you’re reviewing one measurement and MPE when you need an average accuracy across several attempts or data points. Both help you understand and communicate how close your measurements are to the expected values.

    Common Mistakes While Calculating Percent Error

    Even though the percent error formula looks simple, it’s easy to make small mistakes that can lead to big calculation errors. Here are the most common pitfalls—and how to avoid them:

    • Forgetting to use absolute values: Always take the absolute difference between the measured value and the accepted value. Skipping this step can incorrectly show a negative percent error when you only meant to show the size of the error.
    • Using the measured value as the denominator: Remember, the denominator in the percent error formula must always be the accepted (actual) value. Using the measured value instead changes the meaning and accuracy of your result.
    • Mixing up positive and negative percent error: Decide whether you want to show just the magnitude of the error (always positive) or include the direction of the error (positive if your measurement is too high, negative if too low). Be consistent with your choice.
    • Incorrect formula use: Even a small mistake, like missing the multiplication by 100 or swapping values, can change the final answer completely. Double-check each step to make sure you’ve followed the correct formula.

    By being careful with these details, you’ll get percent error results that truly reflect the accuracy of your measurements and make your data more reliable.

    Practice Percent Error Questions

    Test your understanding of percent error calculations with these practice problems. Remember, percent error measures how far a measured value is from the actual (accepted) value, expressed as a percentage.

    Question 1:

    Measured: 98, Actual: 100

    Percent error: ?

    Question 2:

    Measured: 210, Actual: 200

    Percent error: ?

    Question 3:

    Measured: 75, Actual: 80

    Percent error: ?

    Question 4:

    Measured: 150, Actual: 145

    Percent error: ?

    Question 5:

    Measured: 50, Actual: 55

    Percent error: ?

    Question 6:

    Measured: 123, Actual: 120

    Percent error: ?

    Question 7:

    Measured: 500, Actual: 520

    Percent error: ?

    Question 8:

    Measured: 87, Actual: 90

    Percent error: ?

    Question 9:

    Measured: 300, Actual: 280

    Percent error: ?

    Question 10:

    Measured: 42, Actual: 40

    Percent error: ?

    Use these examples to reinforce your understanding!

    Teaching Tips & Learning Resources

    For Educators:

    • Use real-world examples from science and everyday life to make percent error relatable, such as measuring ingredients in cooking or timing races.
    • Emphasize that errors aren’t just mistakes—they help students understand the accuracy and reliability of experiments and improve their techniques.
    • Incorporate interactive tools like online percent error calculators and digital worksheets to engage students and provide instant feedback.
    • Encourage group discussions about why errors happen and how to minimize them in practical settings.

    Resources:

    • Printable classroom posters that visually explain percent error formulas and concepts.
    • Reliable online percent error calculators for students to check their work.
    • Practice quizzes and worksheets to reinforce learning and assess understanding.

    These strategies and materials help students grasp percent error effectively while fostering critical thinking about measurement accuracy.

    Frequently Asked Questions

    Can percent error be negative?

    Yes, percent error can be shown as negative to indicate your measured value was less than the actual value. However, most often it’s reported as a positive number by using the absolute difference.

    Can percent error exceed 100%?

    Absolutely! If your measured value is more than twice the actual value or far from it, percent error can easily exceed 100%. This simply means the measurement is very inaccurate.

    What does a high percent error mean?

    A high percent error means your measured value is far from the accepted or actual value. This usually indicates issues with measurement methods, tools, or experimental conditions.

    Why do we use the actual value in the denominator?

    We use the actual (accepted) value in the denominator because it’s the standard for comparison. It shows how far off your result is from what is considered correct.

    What’s the difference between absolute error and percent error?

    Absolute error is simply the difference between measured and actual values without converting it into a percentage. Percent error shows this difference as a percentage of the actual value, making it easier to interpret accuracy.

    When should I use percent error?

    Percent error is used when you need to check how accurate a measurement, calculation, or estimate is compared to a known or accepted value. It’s common in science labs, engineering, and even simple everyday estimates.

    Can percent error be zero?

    Yes, percent error can be zero when your measured value matches the actual value exactly. This is ideal but rarely happens in real-world experiments.

    What is the accepted value in percent error?

    The accepted value is the true or standard value widely agreed upon by experts or references. It serves as the benchmark to check the accuracy of your measurements.

    What’s the difference between percent error and standard error?

    Percent error shows how far your measurement is from the actual value, while standard error measures how much sample means vary in statistical data. They sound similar but are used for different purposes.

    Why do students often get the wrong percent error?

    Common mistakes include forgetting to use the absolute difference, mixing up measured and actual values, or applying the wrong formula. Following a clear step-by-step method helps avoid these calculation errors.

  • What Is a Remainder?

    What Is a Remainder?

    Ever wondered what’s left after you divide something evenly and it doesn’t quite fit? That leftover number is called a remainder. It plays a critical role in math, especially in division problems. Whether you’re a student, parent, or curious learner, understanding what a remainder is can make arithmetic easier—and faster if you know how to use a remainder calculator.

    Let’s break down the meaning of a remainder, where it appears in real life, how to find it using different methods, and how to use a calculator with remainder to get instant results.

    What Is a Remainder in Math?

    In math, a remainder is the amount left over when one number is divided by another but the result isn’t a whole number. It helps represent incomplete divisions and tells us what’s “left out.”

    Definition of a Remainder

    So, what is the definition of remainder in math? Here’s a simple explanation:

    When you divide 10 by 3, you get 3 as the quotient, but 1 is left over. That “1” is the remainder. In mathematical terms:

    Dividend ÷ Divisor = Quotient with Remainder

    Example:
    10 ÷ 3 = 3 R1

    This means 3 fits into 10 three times, and 1 is left.

    You’ll see this format often in long division problems and even while using a calculator with remainders for division.

    Parts of a Division Problem

    Before diving deeper, let’s review the basic parts of a division equation:

    • Dividend: The number to be divided.
    • Divisor: The number you divide by.
    • Quotient: The result (how many times the divisor fits).
    • Remainder: The leftover amount.

    Example:
    74 ÷ 7 = 10 R4

    Here,
    Dividend = 74, Divisor = 7, Quotient = 10, Remainder = 4

    Understanding what is the quotient and the remainder is key to solving division problems accurately.

    Real-Life Examples of Remainders

    Let’s bring math into the real world.

    Example 1: Sharing Chocolates

    Imagine you have 10 chocolates and 3 friends. You give each friend 3 chocolates. That totals 9 chocolates. You’re left with 1. That leftover chocolate is the remainder.

    Example 2: Packing Apples

    If you pack 46 apples into boxes of 8, how many full boxes can you make?
    46 ÷ 8 = 5 R6

    You’ll have 5 full boxes and 6 apples left over.

    How to Find the Remainder

    There are two main ways:

    1. Manual Method

    Use long division:
    Example:
    52 ÷ 8 = 6 R4

    You divide 52 by 8:

    • 8 fits into 52 six times (8 x 6 = 48)
    • Subtract 48 from 52 = 4

    So, the remainder is 4

    2. Use a Calculator

    Not every calculator shows the remainder by default. But there are many calculators with remainders online. Just enter the dividend and divisor and hit “divide”—you’ll see the quotient and remainder instantly.

    Using a Calculator to Find the Remainder Instantly

    Say goodbye to confusion. A good remainder calculator saves time and improves accuracy. It’s especially useful for students, teachers, and professionals needing fast results.

    Here’s how to use a division calculator with remainders:

    1. Input the dividend (e.g., 74)
    2. Input the divisor (e.g., 7)
    3. Hit enter or calculate
    4. Get results like: Quotient = 10, Remainder = 4

    Remainder in Long Division

    Sometimes, you’re asked to show your work using long division.

    Let’s try:
    6338 ÷ 43

    • 43 goes into 6338 about 147 times
    • Multiply: 147 × 43 = 6321
    • Subtract: 6338 – 6321 = 17

    Remainder = 17

    Long division shows the process, and with tools like a long division with remainder calculator, you can check your answers easily.

    Remainder Theorem (Bonus Concept)

    Ever heard of the Remainder Theorem? It’s used in algebra to find remainders when dividing polynomials.

    Here’s a simplified version:
    If a polynomial f(x) is divided by (x – a), the remainder is f(a).

    Remainders in Synthetic Division

    Synthetic division is a shortcut used in algebra. If the remainder is zero, the divisor divides the polynomial evenly.

    Let’s say you divide a polynomial and ask:
    What is the remainder for the synthetic division problem?

    If you get zero, then it’s a perfect division!

    This is commonly used in higher-level math and can be checked using a synthetic division remainder calculator.

    Properties of Remainders

    Knowing how remainders behave is helpful:

    • The remainder is always smaller than the divisor
    • If the remainder is zero, the division is exact
    • Remainders are whole numbers
    • Remainders are useful in modulo arithmetic (coding and encryption)

    These remaining math rules help you avoid mistakes during exams or coding.

    How to Represent Remainders

    There are different formats to show a remainder:

    • Integer + Remainder: 7 ÷ 3 = 2 R1
    • Decimal: 7 ÷ 3 = 2.33
    • Fraction: 7 ÷ 3 = 2 1/3

    So, if someone asks “What is the remainder 2 as a decimal?”, you can convert it using these methods.

    Fun Activity: Share and Remainder

    Turn math into fun. Try this:

    • Take 20 candies
    • Ask a child to divide them among 6 friends
    • See how many are left

    This teaches the concept of remainder in real life and builds basic math skills.

    Gamifying math makes it stick. Try more sharing activities to help kids learn remainder with activity based examples.

    Common Mistakes with Remainders

    Here’s where students often go wrong:

    • Forgetting to include the remainder
    • Incorrect decimal conversion
    • Using calculators that don’t show remainders

    Charitable Remainder Trust (Clarification Section)

    Some people confuse math remainders with charitable remainder trusts in finance. The two are unrelated.

    If you searched for “what is a charitable remainder annuity trust,” note: this is about estate planning and not relevant to math division.

    Understanding what is a remainder in math is more than a homework question. It’s a skill used in real life—from budgeting to coding to problem-solving.

    Whether you’re learning basic division or polynomial algebra, use a calculator that shows remainder to build speed and confidence.

    FAQs About Remainders

    What is a remainder in math?

    It’s the leftover part when a number doesn’t divide evenly. For example, 10 ÷ 3 = 3 R1.

    How do I find a remainder using a calculator?

    Use a division calculator with remainders. Input your numbers and it shows the remainder instantly.

    What is the remainder of 74 divided by 7?

    74 ÷ 7 = 10 R4

    What is the difference between quotient and remainder?

    The quotient is the number of full times the divisor fits into the dividend. The remainder is what’s left.

    What happens when the remainder is zero?

    It means the number divides evenly with no leftovers.

    How to represent a remainder as a fraction?

    Turn the remainder into a fraction over the divisor.
    Example: 7 ÷ 3 = 2 1/3

    Can I calculate remainders with decimals?

    Yes. But decimals show approximate results. To get exact division, use a calculator with quotient and remainder.

    What is the remainder in synthetic division problems?

    It’s the value left after polynomial division. If the remainder is 0, the divisor is a factor of the polynomial.

    What is a remainder calculator?

    A tool that shows the quotient and remainder when you divide numbers. It’s useful for quick and error-free math.

    How does long division handle remainders?

    In long division, if the divisor doesn’t go into the dividend evenly, the leftover value is written as the remainder.