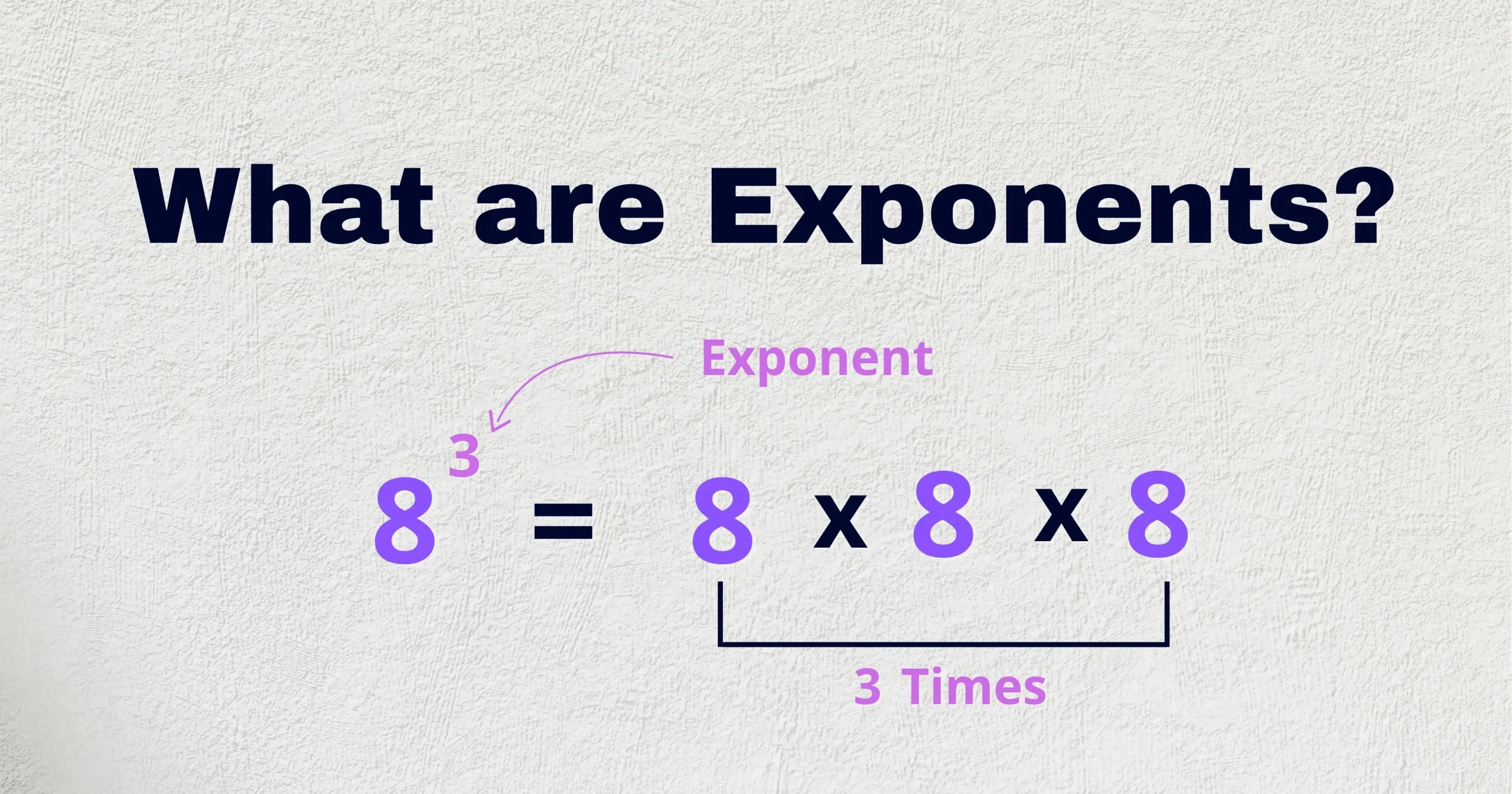Calculus Hub BLog

Blog

  • What Is Hexadecimal? Understanding Base-16 with a Hex Calculator

    The hexadecimal system is more than just tech jargon. It simplifies long binary codes, is crucial in computer science, and plays a vital role in digital color representation, memory addressing, and more. And with a hexadecimal calculator, converting between number systems becomes a breeze. Have you ever looked at a string of numbers and letters like 0x1A3F and wondered what on earth it means? If you’ve ever worked with programming, networking, or digital electronics, chances are you’ve encountered the hexadecimal number system — also known as base-16.

    In this comprehensive guide, we’ll demystify what hexadecimal is, explain why it’s used, show you how to convert between number systems using a hexadecimal calculator, and dive into real-world applications. With step-by-step explanations and helpful tables, you’ll be reading and using hex like a pro.

    Let’s explore everything about hexadecimal, from hexadecimal digits to how you can use a hex calculator to master the base-16 universe.

    Why Do We Use Hexadecimal?

    Computers use binary, but long strings of 0s and 1s are hard for humans to read. That’s why hexadecimal (base-16) is commonly used—it shortens binary while staying true to its values. One hex digit equals four binary digits, making it more compact and readable.

    Key Benefits:

    • Simplifies binary: Hex compresses complex binary into shorter codes.
    • Faster conversions: Converting between binary and hex is quick and direct.
    • Improves readability: Hex is easier to interpret, especially in coding and debugging.
    • Common in tech: Used in memory addresses, HTML color codes (e.g., #FF0000), MAC addresses, and more.

    The need for hexadecimal comes from its efficiency. It bridges the gap between machine language and human understanding, making it essential in programming, networking, and digital design.

    Hexadecimal Number Representation

    So, what is a hexadecimal digit exactly? A hexadecimal number uses 16 unique characters, combining numbers and letters to represent values in base-16. These characters are:

    • 0 = 0
    • 9 = 9
    • A = 10
    • B = 11
    • C = 12
    • D = 13
    • E = 14
    • F = 15

    Because it includes values beyond 9, hexadecimal can represent larger numbers with fewer digits compared to decimal or binary. That’s why this system is especially useful in computing.

    Example:

    Let’s break down the hexadecimal number 2F:

    • 2 = 2 × 16 = 32
    • F = 15 × 1 = 15
    • Total = 32 + 15 = 47 in decimal

    This process demonstrates how hexadecimal digits are weighted by powers of 16, similar to how each digit in decimal is weighted by powers of 10.

    Hexadecimal Conversion Guide

    Understanding how to convert decimal to hexadecimal is crucial when working in programming, networking, or digital electronics. Since hexadecimal is base-16 and decimal is base-10, the conversion process involves repeated division by 16.

    Example: Convert 156 to Hexadecimal

    1. Divide 156 by 16:
    • 156 ÷ 16 = 9 remainder 12
    1. 12 in hexadecimal = C
    2. 9 is written as 9

    So, 156 in hexadecimal is 9C.

    You can also double-check your answer using a reliable decimal to hexadecimal calculator for faster results, especially when dealing with larger numbers.

    Convert Binary to Hexadecimal

    Converting binary to hexadecimal is simple and efficient—just group the binary digits into sets of four (starting from the right) and convert each group to its hex equivalent. This is because 1 hex digit = 4 binary digits, making it a natural match.

    Example: Convert Binary 111010 to Hexadecimal

    1. Pad with leading zeros to make full 4-bit groups: 0011 1010
    2. Group 1: 0011 = 3
    3. Group 2: 1010 = A

    So, 111010 in binary = 3A in hexadecimal.

    For faster conversions, you can use a binary to hexadecimal calculator, especially when dealing with 16-bit or 32-bit binary strings.

    Convert Hexadecimal to Binary

    Each hexadecimal digit maps directly to a 4-bit binary value, which makes hexadecimal to binary conversion fast and accurate. Simply replace every hex digit with its binary equivalent.

    Example: Convert Hex 4F to Binary

    • 4 = 0100
    • F = 1111

    So, 4F in hexadecimal = 01001111 in binary.

    This method works for any hex value, no matter how long. To save time and ensure accuracy with larger values, use a hexadecimal to binary converter or a chart for reference.

    Convert Hexadecimal to Octal

    To convert hexadecimal to octal, it’s best to go through binary as an intermediary step. First, convert each hex digit to its 4-bit binary form, then group the binary into sets of three (from right to left) to get the octal equivalent.

    Example: Convert Hex 1A3 to Octal

    1. Convert each hex digit to binary:
    • 1 = 0001
    • A = 1010
    • 3 = 0011
    • Binary: 000110100011
    1. Group into 3-bit sets (from right):
    • 000 110 100 011
    1. Convert each group to octal:
    • 000 = 0, 110 = 6, 100 = 4, 011 = 3

    So, 1A3 in hexadecimal = 0643 in octal

    To avoid manual conversion errors, you can use a hexadecimal to octal converter, which handles binary steps automatically.

    Convert Octal to Hexadecimal

    To convert octal to hexadecimal, it’s best to go through binary as an intermediary step. First, convert each octal digit to its 3-bit binary form, then group the binary into sets of four (from right to left) to get the hexadecimal equivalent.

    Example: Convert Octal 754 to Hexadecimal

    1. Convert each octal digit to binary:
    • 7 = 111
    • 5 = 101
    • 4 = 100
    • Binary: 111101100
    1. Group into 4-bit sets (from right):
    • 0001 1110 1100
    1. Convert each group to hexadecimal:
    • 0001 = 1, 1110 = E, 1100 = C

    So, 754 in octal = 1EC in hexadecimal

    To avoid manual conversion errors, you can use an octal to hexadecimal converter, which handles the binary steps automatically.

    Using a Hexadecimal Calculator

    A hex calculator quickly converts numbers between hexadecimal, binary, and decimal formats. This saves time and reduces errors compared to manual conversion.

    Who Needs It?

    • Programmers use it for low-level coding and debugging.
    • Network engineers rely on it for working with IP addresses and MAC addresses.
    • Web developers use it to handle hex color codes efficiently.

    Benefits

    • Speeds up conversion tasks
    • Ensures accurate results
    • Supports multiple numbering systems
    • Helpful for learning and quick calculations

    Most calculators allow you to input a number in one format and instantly see the equivalents in others, making it a handy tool for anyone working with different numeric bases.

    ASCII and Hexadecimal

    Every ASCII character corresponds to a unique hexadecimal value. For example:

    • A = 41
    • B = 42
    • Space = 20
    • @ = 40

    This mapping is essential for encoding text data in computers, allowing text to be stored, transmitted, and processed efficiently.

    Example:

    The word “AB @” converts to hex as:

    A → 41

    B → 42

    (space) → 20

    @ → 40

    So, “AB @” in ASCII is represented as the hexadecimal string 41 42 20 40.

    Developers and engineers often use tools like ASCII to hex converters or hex to ASCII translators during debugging, data encoding, and communication protocols to easily switch between readable characters and their hexadecimal representations.

    Real-World Applications of Hexadecimal

    Hexadecimal is widely used in various fields because it offers a compact and readable way to represent binary data.

    Where is Hexadecimal Used?

    • Programming: Memory addresses and pointer values are often shown in hex to simplify reading and debugging.
    • Web Development: Colors are defined using hex color codes like #FF5733, allowing precise control over color in websites and apps.
    • Networking: MAC addresses, which uniquely identify network devices, are represented in hexadecimal format.
    • Debugging: Hex dumps display raw memory content during troubleshooting, making it easier to inspect data.

    Hexadecimal plays a vital role across computing and technology, bridging human-readable and machine-level data.

    Advantages and Disadvantages of Hexadecimal

    Hexadecimal is a base-16 number system widely used in computing and digital electronics. Like any system, it has its strengths and limitations. Understanding these can help you decide when to use hexadecimal effectively.

    Advantages:

    • Compact: Uses fewer digits than binary to represent the same value, making numbers shorter and easier to write.
    • Readable: Easier for humans to read and interpret compared to long binary strings.
    • Efficient: Converts quickly to and from binary since each hex digit corresponds exactly to 4 binary bits.

    Disadvantages:

    • Not Intuitive for Beginners: Hexadecimal is less familiar than decimal, so it can be confusing for those new to number systems.
    • Limited Mathematical Use: Unlike decimal, hex isn’t typically used for everyday arithmetic or calculations.

    Understanding these pros and cons helps decide when hexadecimal is the best choice for representing and working with data.

    Hexadecimal Number Table (0–255)

    Here’s a handy hexadecimal table that compares decimal values with their corresponding hexadecimal equivalents. This table is a useful reference for understanding how numbers translate between these two systems: 

    Decimal Hexadecimal
    000
    100A
    1610
    31 1F
    255FF

    Practice Questions on Hexadecimal

    Test your knowledge and sharpen your skills with these questions:

    1. Convert decimal 245 to hexadecimal.
    2. Convert binary 10101111 to hexadecimal.
    3. Convert hexadecimal 1C3 to decimal.
    4. What is the ASCII hexadecimal value for the character C?
    5. What is the binary equivalent of hexadecimal 2A?
    6. Convert octal 754 to hexadecimal.
    7. Convert hexadecimal FF to decimal.
    8. Convert decimal 1023 to hexadecimal.
    9. What is the hexadecimal representation of the ASCII string “HELLO”?
    10. Convert hexadecimal 7B to binary.
    11. Convert binary 11010101 to hexadecimal.
    12. What is the decimal value of hexadecimal A9?
    13. Convert hexadecimal 3F2 to octal.
    14. Find the hexadecimal equivalent of decimal 4095.
    15. What is the ASCII character for hexadecimal 4D?

    Try working through these to get more comfortable with hexadecimal conversions and related concepts!

    10. FAQs on Hexadecimal

    What is a hexadecimal number?

    A hexadecimal number is a number expressed in base-16, using digits from 0 to 9 and letters A to F. It is commonly used in computing to represent binary data in a more readable and compact form.

    Why do we use hexadecimal instead of binary?

    Hexadecimal simplifies binary notation by grouping every four bits into one hex digit. This makes reading, writing, and interpreting long binary strings faster and less error-prone, especially in coding and debugging.

    How do you convert a decimal number to hexadecimal?

    To convert decimal to hexadecimal, divide the number by 16 and track the remainders until the result is zero. The remainders, read in reverse, give the hex equivalent—or use a decimal to hexadecimal calculator for a quick result.

    What does 0x mean in hexadecimal notation?

    The prefix 0x indicates that the number following it is in hexadecimal format. It’s widely used in programming languages like C, C++, and Java to distinguish hex values from decimal or binary numbers.

    How is hexadecimal used in web design?

    In HTML and CSS, hexadecimal color codes are used to define colors, such as #FFFFFF for white or #000000 for black. Each pair of digits in the 6-character hex code represents the intensity of red, green, and blue (RGB).

    What are the hexadecimal digits from 0 to F?

    The hexadecimal digits are: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. While 0 to 9 match regular decimal digits, A to F stand for values 10 through 15.

    How do you convert hexadecimal to binary?

    To convert hexadecimal to binary, replace each hex digit with its 4-bit binary equivalent. For example, hex 2F becomes 00101111 in binary.

    What is ASCII to hexadecimal conversion?

    ASCII to hexadecimal conversion translates text characters into their hex equivalents. For example, the letter ‘C’ has an ASCII value of 67, which converts to 43 in hexadecimal.

    Is hexadecimal used in IP or MAC addresses?

    Yes, hexadecimal is used in MAC addresses (e.g., 00:1A:2B:3C:4D:5E) and IPv6 addresses (e.g., 2001:0db8:85a3:0000:0000:8a2e:0370:7334). It provides a more efficient and readable way to represent long binary strings.

    What is the difference between a hexadecimal calculator and a converter?

    A hexadecimal calculator allows you to perform arithmetic operations directly in the hex system. A converter is designed to change values from one base (like decimal or binary) into hexadecimal and vice versa.

  • How to Calculate Percentage

    The term “percentage” is derived from the Latin word “per centum”, which means “by the hundred”. So, to Calculate percentage, the whole part is taken as 100. Percentages are everywhere – from calculating exam scores to shopping discounts and financial growth. If you’ve ever wondered how to calculate the percent of a number or turn a value into a percentage, this complete guide will walk you through every step. Whether you’re a student, professional, or just curious, mastering percentages is essential.

    For example, if a student scores 36 out of 60 in science, then the percentage can be calculated by expressing the marks obtained as a fraction of the total marks, and multiplying the result by 100.

    i.e.,
    percentage of marks = $$[
    \left( \frac{36}{60} \right) \times 100 = 60\%
    ]$$

    What is a Percentage?

    A percentage is a number or ratio expressed as a fraction of 100. It’s denoted by the symbol “%” and is used to show proportions, comparisons, and changes in values. For example, 40% means 40 out of 100.

    Understanding Percentage

    Percentages simplify how we talk about parts of a whole. Whether you’re figuring out what portion of your salary is spent on rent or what percent of your class passed the test, percentages offer an easy way to interpret and compare numbers.

    Common Uses of Percentages in Real Life

    • Discounts and Offers: 30% off a product
    • Exam Scores: 85% in math
    • Finance: 6% interest on savings
    • Data Analysis: Survey results, growth trends

    Percentage Formula with Example

    The standard formula for calculating percentage is:

    Percentage (%) = $$[
    \left( \frac{\text{Part}}{\text{Whole}} \right) \times 100
    ]$$

    Example: If you scored 45 out of 60 in a test, your percentage is:

    $$[
    \left( \frac{45}{60} \right) \times 100 = 75\%
    ]$$

    How to Calculate Percentage of a Number

    To find a specific percentage of a value, use this formula:

    Percentage Value = $$[
    \left( \frac{\text{Percentage}}{100} \right) \times \text{Total Number}
    ]$$

    Example: $$[
    20\% \text{ of } 150 = \left( \frac{20}{100} \right) \times 150 = 30
    ]$$

    How to Calculate Percentage of Marks

    Use the same formula:

    Marks Percentage = $$[
    \left( \frac{\text{Marks Obtained}}{\text{Total Marks}} \right) \times 100
    ]$$

    Example: $$[
    \left( \frac{68}{80} \right) \times 100 = 85\%
    ]$$

    Another Example: If a student scores 15 out of 50 in math, then:

    Percentage = $$[
    \left( \frac{15}{50} \right) \times 100 = 30\%
    ]$$

    Another Example: If a student scores 36 out of 60 in science, then:

    Percentage = $$[
    \left( \frac{36}{60} \right) \times 100 = 60\%
    ]$$

    How to Calculate Percentage of Money

    For tips, taxes, and interest:

    Example: $$[
    18\% \text{ tip on } \$50 = \left( \frac{18}{100} \right) \times 50 = \$9
    ]$$

    How Do I Calculate What Percentage One Number Is of Another?

    Use this reverse formula:

    Percentage = $$[
    \left( \frac{\text{Part}}{\text{Whole}} \right) \times 100
    ]$$

    Example: $$[
    30 \text{ is what percent of } 120? \quad \left(\frac{30}{120}\right) \times 100 = 25\%
    ]$$

    How to Calculate Total Given a Percentage

    When you’re given a part and the percentage, and need to find the whole:

    Total = $$[
    \text{Whole} = \frac{\text{Part}}{\left(\frac{\text{Percentage}}{100}\right)}
    ]$$

    Example: $$[
    \text{Number} = \frac{50}{0.25} = 200
    ]$$

    How to Calculate Percentage Off a Value (Discount)

    To calculate how much you save:

    Discount = $$[
    \left(\frac{\text{Discount \%}}{100}\right) \times \text{Original Price}
    ]$$

    Example: $$20\% \text{ off } \$80 = \left(\frac{20}{100}\right) \times 80 = \$16$$

    Final Price = $80 – $16 = $64

    How to Convert a Value into a Percentage

    Use this formula:

    $$\left(\frac{\text{Value}}{\text{Total}}\right) \times 100$$

    Example: $$\left(\frac{45}{90}\right) \times 100 = 50\%$$

    What is the Formula for Converting to Percentages?

    Standard formula:

    Percentage = $$\left(\frac{\text{Part}}{\text{Whole}}\right) \times 100$$

    How to Quickly Calculate Percentages

    • 10% of a number: Move the decimal one place left.
    • 5%: Half of 10%
    • 1%: Move two places left
    • 20%: Double 10%

    Example: $$20\% \text{ of } 80 = 8 + 8 = 16$$

    Percentage Increase and Decrease

    Percentage Increase:

    $$\left( \frac{\text{New Value} – \text{Original Value}}{\text{Original Value}} \right) \times 100$$

    Percentage Decrease:

    $$\left( \frac{\text{Original Value} – \text{New Value}}{\text{Original Value}} \right) \times 100$$

    Percentage Difference Calculator

    To find the percentage difference between two values:

    $$\left( \frac{|\text{Value}_1 – \text{Value}_2|}{\frac{\text{Value}_1 + \text{Value}_2}{2}} \right) \times 100$$

    Example: Difference between 60 and 80 = $$\left( \frac{20}{70} \right) \times 100 \approx 28.57\%$$

    Conversion Between Percentages, Decimals, and Fractions

    • Decimal to Percent: Multiply by 100 (0.25 = 25%)
    • Percent to Decimal: Divide by 100 (75% = 0.75)
    • Fraction to Percent: (3/4) × 100 = 75%
    • Percent to Fraction: 60% = 60/100 = 3/5

    Percentage Formula in Excel

    Use the formula: =$$\left( \frac{\text{Part}}{\text{Total}} \right) \times 100$$

    Example: =$$\left( \frac{40}{200} \right) \times 100 = 20\%$$

    Percentage Calculator Tool

    Use our Percentage Calculator to save time:

    • Calculate percentage of a number
    • Find what percent one number is of another
    • Work out discounts and markups instantly

    Now that you know how to calculate percentages of numbers, marks, money, and more, you can confidently apply these formulas in school, work, or daily life. From calculating tips at dinner to analyzing your grades or tracking business growth – percentages are a powerful tool. Use our built-in Percentage Calculator to get answers fast, or practice the formulas manually to sharpen your math skills!

    Frequently Asked Questions 

    How do I calculate a percentage?

    To calculate a percentage, use: $$\left( \frac{\text{Part}}{\text{Whole}} \right) \times 100$$

    How do I find the percentage of a value?

    In order to find the percentage of a value, use: $$\left( \frac{\text{Discount \%}}{100} \right) \times \text{Price}$$.

    How can I calculate the percentage of marks?

    Percentage of marks can be calculated by: $$\left( \frac{\text{Marks Obtained}}{\text{Total Marks}} \right) \times 100$$

    Can the percentage be more than 100?

    Yes, especially in growth comparisons or values exceeding the total.

    What is the difference between percentage and percent?

    “Percent” is used with a number; “percentage” refers to the concept.

    How to convert decimals and fractions to percentages?

    Multiply decimal or fraction by 100.

    How to calculate reverse percentage?

    Total = $$\frac{\text{Part}}{\left( \frac{\text{Percentage}}{100} \right)}$$

    How to calculate a value into percentage?

    Divide the value by the total and multiply by 100.

    How to quickly calculate percentages without a calculator?

    Use shortcuts like moving decimal points, doubling 10%, etc.

  • Introduction to Fraction and Calculator Guide

    Introduction to Fraction and Calculator Guide

    Ever sliced a pizza into 8 pieces and eaten 3? Congratulations, you just used a fraction. Fractions are all around us — in recipes, while measuring distances, splitting bills, or understanding discounts. They appear in cooking, shopping, construction, and even in time management. Yet, for many learners, fractions seem confusing at first.

    But here’s the good news: once you understand the basic structure and use of fractions, they become incredibly helpful tools. Whether you’re calculating a discount, dividing a bill, or baking a cake, knowing how fractions work makes life easier and math more logical. 

    This guide to fractions explain the parts, explore different types of fractions, and show how to perform operations with them. By the end, you’ll not only understand fractions but be able to use them confidently in everyday life and academic settings.

    Understanding the Parts of a Fraction

    Let’s begin with a basic definition. A fraction represents a part of a whole. It is a way to express numbers that are not whole numbers and is written as $$\frac{a}{b}$$, where:

    • a is the numerator, and
    • b is the denominator.

    The numerator indicates how many parts we have, while the denominator tells us how many equal parts the whole is divided into. This basic structure is used everywhere in math and real life.

    Example: In $$\frac{3}{4}$$,

    • 3 is the numerator: the number of parts you have,
    • 4 is the denominator: the total parts the whole is split into.

    Understanding this lays the groundwork for all fraction operations and applications.

    Types of Fractions

    Fractions come in many forms, and understanding these variations is crucial for both solving problems and applying them in real-world contexts. Here are the most commonly used types of fractions:

    Proper Fractions

    A proper fraction is one where the numerator is smaller than the denominator. This means the fraction represents a quantity less than one whole.

    Examples:

    • $$\frac{3}{5}$$ (3 parts out of 5)
    • $$\frac{7}{8}$$ (7 parts out of 8)

    Proper fractions are most commonly used in everyday scenarios, such as sharing food or time.

    Improper Fractions

    An improper fraction has a numerator that is equal to or greater than its denominator, which means it represents a quantity equal to or greater than one.

    Examples:

    • $$\frac{7}{4}$$ (greater than 1)
    • $$\frac{10}{6}$$ (greater than 1.5)

    Improper fractions are frequently converted into mixed numbers to make them easier to interpret.

    Mixed Fractions

    A mixed fraction, or mixed number, combines a whole number with a proper fraction. These are particularly helpful in measurements, cooking, and carpentry.

    Examples:

    • $$2\frac{1}{3}$$ (2 whole units and 1/3 more)
    • $$5\frac{2}{5}$$ (5 whole units and ⅖ more)

    Mixed numbers are often used in recipes (e.g., $$1\frac{1}{2}$$cups of milk) or construction (e.g., $$4\frac{3}{4}$$inches).

    Like & Unlike Fractions

    Like fractions have the same denominator and are easy to add or subtract directly.

    • Example:  ⅜ and ⅝

    Fractions have different denominators and must be converted to a common denominator before you can perform operations.

    • Example: ⅓ and ¾

    Knowing the difference between like and unlike fractions is essential when performing arithmetic operations.

    Equivalent Fractions

    Equivalent fractions are different fractions that represent the same part of a whole. They are created by multiplying or dividing the numerator and denominator by the same number.

    Examples:

    $$\frac{1}{2} = \frac{2}{4} = \frac{4}{8}$$

    Equivalent fractions are useful when comparing values or simplifying problems.

    Unit Fractions

    A unit fraction has a numerator of 1. It represents one single part of a whole and is considered the building block for other fractions.

    Examples:

    • $$\frac{1}{3}$$
    • $$\frac{1}{100}$$

    Unit fractions are often used in division and when learning basic fraction concepts.

    Complex Fractions

    A complex fraction has a fraction in the numerator, denominator, or both. These types often arise in algebra and higher-level mathematics.

    Example:

    $$\frac{\frac{3}{4}}{\frac{5}{6}}$$

    Solving complex fractions requires multiple steps, including finding reciprocals and simplifying.

    Decimal Fractions

    A decimal fraction is a fraction where the denominator is a power of 10 and is usually expressed in decimal form.

    Examples:

    • $$\frac{7}{10}$$ = 0.7
    • $$\frac{12}{1000}$$ = 0.125

    These fractions are used widely in currency, science, and engineering.

    Improper to Mixed Conversion

    Sometimes it’s necessary to convert an improper fraction to a mixed number to better understand the quantity.

    Example:

    $$\frac{9}{4} = 2\frac{1}{4}$$

    This type of conversion is especially helpful in visual estimation and measurement tasks.

    Each type of fraction serves a specific purpose and becomes more useful when you know when and how to apply them. Mastery of these variations is key to being fraction fluent.

    Fractions on a Number Line

    Visualizing fractions on a number line is one of the best ways to understand what a fraction truly represents. It helps learners develop a sense of size, order, and value of fractions compared to whole numbers.

    How to Plot Fractions on a Number Line

    Let’s start with a basic example:

    Plot $$\frac{9}{4}$$ on a number line between 0 and 1:

    • Step 1: Draw a horizontal line.
    • Step 2: Mark 0 on the left end and 1 on the right end.
    • Step 3: Since the denominator is 2, divide the space between 0 and 1 into 2 equal parts.
    • Step 4: The point halfway between 0 and 1 is $$\frac{1}{2}$$.

    Now try plotting $$\frac{3}{4}$$:

    • Divide the segment between 0 and 1 into 4 equal parts.
    • Count three steps from 0.
    • You land at $$\frac{3}{4}$$.

    This method works for any fraction — just divide the space between 0 and 1 (or any two whole numbers) based on the denominator.

    Properties of Fractions

    Fractions follow fundamental math rules, called properties of fractions. Knowing these helps in simplifying and solving problems faster.

    Commutative Property

    This applies to addition and multiplication:

    • $$\frac{a}{b} + \frac{c}{d} = \frac{c}{d} + \frac{a}{b}$$
    • $$\frac{a}{b} \cdot \frac{c}{d} = \frac{c}{d} \cdot \frac{a}{b}$$

    Example:

    $$\frac{1}{3} + \frac{2}{5} = \frac{2}{5} + \frac{1}{3}$$

    Both give the same result: $$\frac{11}{15}$$

    Associative Property

    You can regroup the fractions when adding or multiplying:

    • $$\left( \frac{a}{b} + \frac{c}{d} \right) + \frac{e}{f} = \frac{a}{b} + \left( \frac{c}{d} + \frac{e}{f} \right)$$
    • $$\left( \frac{a}{b} \times \frac{c}{d} \right) \times \frac{e}{f} = \frac{a}{b} \times \left( \frac{c}{d} \times \frac{e}{f} \right)$$

    Identity Property

    • Additive identity: $$\frac{a}{b} + 0 = \frac{a}{b}$$
    • Multiplicative identity: $$\frac{a}{b} \times 1 = \frac{a}{b}$$

    Understanding these fraction identities makes operations smoother and helps identify shortcuts during calculations.

    Rules for Simplifying Fractions

    Simplifying a fraction means reducing it to its lowest terms — the form in which numerator and denominator have no common factors (other than 1).

    To simplify:

    • Find the greatest common divisor (GCD) of the numerator and denominator.
    • Divide both by the GCD.

    Example:

    Simplify $$\frac{15}{25}$$

    GCD of 15 and 25 is 5

    15 ÷ 5 = 3, and 25 ÷ 5 = 5

    So, simplified fraction = $$\frac{3}{5}$$

    This step is essential before doing other operations and is frequently needed when working with equivalent fractions or comparing values.

    How to Add Fractions

    Adding fractions depends on whether the denominators are like or unlike.

    Case 1: Like Denominators

    If both fractions have the same denominator, simply add the numerators.

    Example:

    $$\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} = \frac{5}{7}$$

    Case 2: Unlike Denominators

    Use the Least Common Denominator (LCD) to convert them into like fractions.

    Steps:

    1. Find the LCD of the two denominators.
    2. Convert each fraction.
    3. Add the numerators.

    Example:

    $$\frac{1}{4} + \frac{1}{6}$$

    LCD = 12

    $$\frac{1}{4} = \frac{3}{12}, \quad \frac{1}{6} = \frac{2}{12}$$

    So, $$\frac{3}{12} + \frac{2}{12} = \frac{5}{12}$$

    This method of adding fractions with different denominators is essential for advanced arithmetic.

    Adding Fractions with Different Denominators

    This specific case requires using the LCM (least common multiple) of the denominators. It’s often one of the trickiest operations, so let’s break it down clearly.

    Example:

    Add $$\frac{5}{6} + \frac{2}{9}$$

    LCM of 6 and 9 = 18

    Convert:

    $$\frac{5}{6} = \frac{15}{18}$$

    $$\frac{2}{9}= \frac{4}{18}$$

    Add:

    $$\frac{15}{18}+ \frac{4}{18}= \frac{19}{18} = 1\frac{1}{18}$$ (Improper converted to mixed)

    How to Subtract Fractions

    Subtracting fractions also depends on whether the denominators are like or unlike.

    Case 1: Like Denominators

    If both fractions have the same denominator, subtract the numerators directly and keep the denominator the same.

    Example:

    • $$\frac{5}{9} – \frac{2}{9} = \frac{5 – 2}{9} = \frac{3}{9} = \frac{1}{3}$$

    Steps:

    1. Find the LCD of the two denominators.
    2. Convert each fraction to an equivalent fraction with the LCD.
    3. Subtract the numerators.
    4. Simplify the result if needed.

    Example:

    • $$\frac{2}{3} – \frac{1}{4}$$

    LCD of 3 and 4 = 12

    • $$\frac{2}{3} = \frac{8}{12}, \quad \frac{1}{4} = \frac{3}{12}$$

    Now subtract:

    • $$\frac{8}{12} – \frac{3}{12} = \frac{5}{12}$$

    This method of subtracting fractions with different denominators is essential for solving real-world and academic math problems.

    Subtracting Fractions with Different Denominators

    This case also requires using the LCM (Least Common Multiple) of the denominators. It’s a crucial skill in fraction subtraction and follows a simple step-by-step method.

    Example:

    Subtract:

    $$\frac{7}{10} – \frac{1}{4}$$

    Step 1: Find the LCM of the denominators

    LCM of 10 and 4 = 20

    Step 2: Convert both fractions to like denominators

    $$\frac{7}{10} = \frac{14}{20}$$

    $$\frac{1}{4} = \frac{5}{20}$$

    Step 3: Subtract the numerators

    $$\frac{14}{20} – \frac{5}{20} = \frac{9}{20}$$

    Final Answer:

    $$\frac{9}{20}$$

    This method of subtracting fractions with different denominators ensures accuracy and is essential for mastering fraction operations in both academic and real-life contexts.

    Multiplying Fractions

    Multiplying fractions is the simplest operation.

    Just multiply:

    • Numerators together
    • Denominators together

    Example:

    $$\frac{2}{3} \times \frac{3}{5} = \frac{6}{15} = \frac{2}{5}$$

    If multiplying mixed numbers:

    1. Convert them into improper fractions.
    2. Multiply as usual.
    3. Simplify.

    Example:

    $$1\frac{1}{2} \times \frac{2}{3} = \frac{3}{2} \times \frac{2}{3} = 1$$

    1.  Dividing Fractions

    To divide fractions, flip the second fraction and multiply.

    This is called the reciprocal method or invert and multiply.

    Steps:

    1. Invert the second fraction.
    2. Multiply both.

    Example:

    $$\frac{3}{4} \div \frac{2}{5} = \frac{3}{4} \times \frac{5}{2} = \frac{15}{8} = 1\frac{7}{8}$$

    This method is often taught as “Keep, Change, Flip” — keep the first, change the sign to multiplication, and flip the second.

    Real-Life Examples of Fractions

    Fractions play a big role in daily activities:

    • Cooking: Recipes often use $$\frac{5}{9} tsp$$, $$\frac{1}{3} cup$$, etc.
    • Shopping: Discounts like 25%off = $$\frac{1}{4}$$ off
    • Travel: “Halfway there” = $$\frac{1}{2}$$ of the journey
    • Banking: Interest rates or dividends often appear in fractions
    • Construction: Tools often measure in $$\frac{1}{8}$$ or $$\frac{1}{16}$$ inches

    Understanding fractions in real life shows their practical value — far beyond textbooks.

     Converting Fractions to Decimals

    Fractions to decimals conversion is very useful for precise calculations.

    Method 1: Long Division

    Divide numerator by denominator.

    Example:

    $$\frac{5}{8}$$ = 5 ÷ 8 = 0.625

    Method 2: Using a Calculator

    Input numerator and denominator and press the divide (÷) button.

    This is a great trick when learning how to convert fractions to decimals quickly and accurately.

     Solved Examples on Fractions

    Here are a few solved fraction examples:

    1. Add $$\frac{3}{4} + \frac{2}{5}$$

    LCM = 20 → $$\frac{15}{20} + \frac{8}{20} = \frac{23}{20} = 1\frac{3}{20}$$

    1. Subtract $$\frac{7}{8} – \frac{3}{4}$$

    LCM = 8 → $$\frac{7}{8} – \frac{6}{8} = \frac{1}{8}$$

    1. Multiply $$\frac{2}{5} \times \frac{3}{7} = \frac{6}{35}$$
    2. Divide $$\frac{4}{9} \div \frac{2}{3} = \frac{4}{9} \times \frac{3}{2} = \frac{12}{18} = \frac{2}{3}$$

    Practicing various problems helps master fractions in math.

    Fraction Calculator Guide

    An online fraction calculator is a great learning tool. Whether you’re adding, subtracting, multiplying, or dividing fractions, it gives you answers instantly.

    How to Use a Fraction Calculator

    1. Input the first fraction.
    2. Choose an operation (+, −, ×, ÷).
    3. Input the second fraction.
    4. Click calculate.

    These calculators also help with simplifying fractions and converting to decimals.

    Benefits of Using a Fraction Calculator

    • Speed: Instant answers.
    • Accuracy: No manual errors.
    • Learning Support: Helps check homework.
    • Convenience: Easy to use for all operations.
    • Visual Aid: Some calculators show steps.

    These tools make fraction calculation easy for learners of all levels.

    Practice Questions on Fractions

    Here are some fraction practice questions to test your skills:

    1. Add: $$\frac{1}{2} + \frac{1}{3}$$
    2. Subtract: $$\frac{5}{6} – \frac{2}{9}$$
    3. Multiply: $$\frac{3}{4} \times \frac{1}{2}$$
    4. Divide: $$\frac{7}{8} \div \frac{1}{4} = \frac{7}{8} \times \frac{4}{1} = \frac{28}{8} = \frac{7}{2}$$
    5. Simplify: $$\frac{16}{24}$$
    6. Convert to improper: $$1\frac{2}{5}$$
    7. Convert to decimal: $$\frac{3}{4}$$
    8. Compare: Which is larger, $$\frac{2}{3} or \frac{3}{5}$$?
    9. Find equivalent: $$\frac{2}{6} = \frac{?}{3}$$
    10. Plot on a number line: $$\frac{5}{8}$$

    Frequently Asked Questions (FAQs)

    1. What is a fraction in math?

    A fraction is a number that represents a part of a whole. It is written in the form of numerator over denominator, like $$\frac{3}{4}$$.

    2. What are the main types of fractions?

    The three main types of fractions are proper, improper, and mixed fractions. Each type represents different relationships between the numerator and denominator.

    3. What is a proper fraction?

    A proper fraction has a numerator smaller than the denominator. It always represents a value less than 1.

    4. What is an improper fraction?

    An improper fraction has a numerator greater than or equal to the denominator. It represents a value equal to or more than 1.

    5. What is a mixed fraction?

    A mixed fraction is a combination of a whole number and a proper fraction, like $$2\frac{1}{13}$$. It shows a quantity greater than one.

    6. How do you simplify a fraction?

    To simplify a fraction, divide both the numerator and denominator by their greatest common divisor (GCD). The result is the fraction in its lowest terms.

    7. How do you add fractions with different denominators?

    Find the least common denominator (LCD), convert both fractions to like denominators, and then add the numerators. Always simplify the result if possible.

    8. How do you subtract fractions with different denominators?

    Use the same process as adding: find the LCD, convert the fractions, and subtract the numerators. Simplify the final answer to its lowest form.

    9. How do you multiply fractions?

    Multiply the numerators together and then the denominators. Simplify the resulting fraction if needed.

    10. How do you divide fractions?

    Flip the second fraction (find its reciprocal), then multiply it by the first. This is known as the “invert and multiply” rule.

    11. What are equivalent fractions?

    Equivalent fractions are fractions that look different but represent the same value. For example, $$\frac{1}{2}$$ is equivalent to $$\frac{2}{4}$$ or $$\frac{3}{6}$$.

    12. What is a unit fraction?

    A unit fraction has a numerator of 1 and a whole number as the denominator, like $$\frac{1}{5}$$. It represents one equal part of a whole.

    13. How are fractions used in real life?

    Fractions are used in cooking, time management, shopping discounts, construction measurements, and more. They help divide quantities into smaller parts.

    14. How do you convert a fraction to a decimal?

    Divide the numerator by the denominator using long division or a calculator. The result is the decimal form of the fraction.

    15. What is a fraction calculator and how does it help?

    A fraction calculator performs operations like addition, subtraction, multiplication, and division of fractions quickly. It improves accuracy and saves time, especially for complex problems.

  • What Are Exponents? Rules, Examples & Calculator Guide

    What Are Exponents? Rules, Examples & Calculator Guide

    Suppose, you are calculating the Weight of rice you produced this year. It weighed 10000000000 kg. So, while noting, writing 109 Kg will be easier than writing 10000000000 kg. So here, 9 is the exponent of 10. Which means, 10 is multiplied 9 times by itself. It can be broken down as 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 = 109 . This example is read as 9 is the power of 10 or 10 to the power 9. 

    The process of expressing large numbers in terms of power is called exponents. The exponent of a number indicates the total times to use that number in a multiplication. 7×7×7 can be expressed as 73 because 7 is multiplied 3 times by itself which results in 343. The 3 in this example is called ‘exponents’ or ‘power’ which tells how many times 7 can be multiplied.  

    Let’s take few more examples:

    82 = 8×8 = 64

    (Here, 2 is the exponent which tells 8 can be multiplied 2 times.)

    63 = 6×6×6 = 216

    (Here, The exponent 3 tells that 6 should be multiplied 3 times.)

    But, there are some exceptional cases. Such as:

    4 0 = 1

    (We must keep in mind that when the exponent is 0, the result will be 1.)

    Exponents are commonly used in:

    • Scientific notation (e.g., 6.02 x 1023 )
    • Algebra and calculus
    • Computer science and data analysis
    • Real-world applications like compound interest and population growth

    Exponents in Math: Definition & Basics

    Exponents has a simple definition, it tells you how many times to multiply the base by itself.

    Terms to understand:

    • Base: The number being multiplied. 
    • Exponent (or power): Tells how many times the base is used as factor.

    Example: 53 = 5 x 5 x 5 = 125

    This is read as “Five raised to the power of three” or “Five Cube”

    Why Are Exponents Important in Math?

    Exponents help express very large or very small numbers in a compact form. They’re essential for:

    • Simplifying calculations
    • Expressing patterns and repeated multiplication
    • Calculating growth in finance and science
    • Programming and algorithms

    Basic Exponent Rules (With Examples)

    There are some laws of exponents in mathematics. 

    Product Rule

    am x an = am+n  

    Example:

    23 x 24  = 23+4 = 27 = 128

    Quotient rule

    $$\frac{a^m}{a^n} = a^{m-n}$$ (when a ≠ 0) Example: $$\frac{5^5}{5^2} = 5^{5-2} = 5^3 = 125$$

    Zero Exponent Rule

    $$a^0 = 1$$ (when a ≠ 0) Example: $$7^0=1$$ 

    Negative Exponent Rule

    $$a^{-n} = \frac{1}{a^n}$$ Example: $$3^{-2} = \frac{1}{3^2} = \frac{1}{9}$$

    Power of a Power Rule

    $$(a^m)^n = a^{m \cdot n}$$ Example: $$(2^3)^2=2^(3 \cdot2)=2^6=64$$

    Power of a Product Rule

    $$(ab)^n = a^n \cdot b^n$$ Example: $$(2 \cdot 3)^2 = 2^2 \cdot 3^2 = 4 \cdot 9 = 36$$

    Power of a Quotient Rule

    $$\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}$$ Example: $$\left(\frac{4}{2}\right)^2 = \frac{4^2}{2^2} = \frac{16}{4} = 4$$


    Fractional Exponents

    $$a^{\frac{m}{n}} = \sqrt[n]{a^m}$$

    Example:

    $$8^{\frac{1}{3}} = \sqrt[3]{8} = 2$$


    Common Mistakes with Exponents 

    There are some common mistakes that exponents learners make: 

    • Confusing base vs. exponent: 23 ≠ 32 
    • Adding exponents when bases differ: 22 + 32 ≠ 54  
    • Wrong sign handling in negative exponents: -22 ≠ (-2)2 

    Exponent Calculator (Interactive Tool)

    Use this calculator to compute any exponent quickly:

    • Enter base and exponent
    • Click Calculate
    • Get instant result with simplified expression

    How to Use the Exponent Calculator:

    1. Input a base number (e.g., 5)
    2. Input exponent (e.g., 3)
    3. Click “Calculate”
    4. Output:

    Try it for fractional or negative exponents too!

    Advanced Topics: Exponents with Variables & Logs

    Exponents with Variables

    $$x^a \cdot x^b = x^{a+b}$$ Often used in algebraic expressions.

    Derivatives of Exponential Expressions

    In calculus, the derivative of $$a^x$$ is: $$\frac{d}{dx} \left( a^x \right) = a^x \ln(a)$$

    Logarithms and Exponents

    $$[
    \log_b \left( a^c \right) = c \cdot \log_b(a)
    ]$$

    Logs are the inverse of exponentiation.

    Exponents are powerful tools in both basic and advanced mathematics. By understanding their rules—like the product, quotient, and power laws—you can simplify complex expressions, solve problems faster, and grasp algebra and calculus concepts with ease.

    Don’t forget to use the Exponent Calculator above for quick and accurate solutions to any exponent-related math problem.

    FAQs on Exponents

    1. What is an exponent in math?
    An exponent shows how many times a number is multiplied by itself.

    2. What are the rules of exponents?
    They include product, quotient, zero, negative, power, and fractional rules.

    3. How do you multiply exponents?
    Add exponents if bases are same: $$a^m \cdot a^n = a^{m+n}$$

    4. What does a negative exponent mean?
    It means reciprocal: $$a^{-n} = \frac{1}{a^n}$$

    5. Can exponents be fractions?
    Yes. $$a^{\frac{1}{2}} = \sqrt{a}$$ , etc.

    6. How to type an exponent?
    Use superscript in Word or ^ symbol (e.g., 2^3).

    7. What is the zero exponent rule?
    Any non-zero number to the power of 0 equals 1.

    8. What’s the difference between exponents and powers?
    They are often used interchangeably, but “power” can refer to the whole expression an.

    9. How to simplify exponents?
    Use exponent laws to combine and reduce expressions.

    10. Is there a calculator for exponents?
    Yes, use the tool above or a scientific calculator.

  • What Is Binary? Meaning, Uses in Computing, and Binary Calculator Guide

    What Is Binary? Meaning, Uses in Computing, and Binary Calculator Guide

    We believe that the Binary number system came into existence when computers were invented. But the truth is different. Though it seems like it is connected with modern invention, the binary number system was invented back thousands of years ago. Ancient logic used broken and unbroken lines (representing 0 and 1) to symbolize yin and yang, effectively forming a primitive binary framework dated in China. 

    Later in the 17th century, mathematician and philosopher Gottfried Wilhelm Leibniz explained a system that used only two digits—0 and 1—and showed how any numerical value could be represented using just these two symbols. This concept later became a foundation for Digital Computing.

    Now, in the 20th century, Engineers adopted the Binary Number System as the primary computer language. It operates using two states: on (1) and off (0). Here in this article, we’ll be covering the Meaning, uses and guide to the calculator. 

    What Is the Binary Number System? 

    Basically there are 4 number systems and Binary is one of them. The binary number system is a base-2 numeral system. Bi stands for 2 which makes clear that it is represented by 2 digits that are 0 (zero) and 1 (one). It is applied in all the latest computers and computer based devices around the globe. Binary is the perfect medium to process and store the strong data easily and concisely. It is the fundamental language of computers reflecting the on-off states of electrical circuits.  

    Example of a Binary Number

    Let’s take the binary number 1010.

    To convert it to decimal:

    • (1 × 2³) + (0 × 2²) + (1 × 2¹) + (0 × 2⁰)
    • = (1 × 8) + (0 × 4) + (1 × 2) + (0 × 1)
    • = 8 + 0 + 2 + 0
    • = 10

    👉 So, binary 1010 = decimal 10.

    Binary vs Decimal: What’s the Difference?

    Binary number system (base-2)  and decimal number system (base-10)  are two different ways of representing value. The difference is, binary is mostly used in computers whereas decimal is implemented in real life.

    Decimal includes the whole numbers and the fractional part separated by a decimal point (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Whereas Binary expresses numbers in just 2 terms (0, 1).  

    Here’s the details of base-2 vs base-10 in the table.

    FeatureBinary (Base-2)Decimal (Base-10)
    Number Base210
    Digits Used0, 10 to 9
    Used ByComputers, digital systemsHumans, everyday math
    Place ValuesPowers of 2 (1, 2, 4, 8…)Powers of 10 (1, 10, 100…)
    Example1011 = 11 in decimal11 = 11 in decimal
    Efficiency in ComputingHighly efficientInefficient for digital logic
    Storage RepresentationOn/Off (1/0) statesNot directly used

    Why do Computers use binary over decimal? 

    Computers hardware is built using millions of tiny electric switches (also called transistors) which can only be ON or OFF. These states match with 1 and 0 where 1 is On and 0 is Off.

    Just imagine, you got to switch off the light. There’s one switch where there’s just an on/off button, and there’s another switch with 10 buttons. Which one will you choose? Obviously the on/off one right. This is why binary representation wins over decimals in computers.

    These states are represented in various pairs like:

    • On/Off
    • High/Low
    • True/False
    • 1/0 (most relevant here)

    Since, here’s why Binary is ideal for computing. 

    • Simplicity: Binary logic is simple and reliable for circuits.
    • Low Error Rate: It’s easier to detect and correct errors with binary signals.
    • Efficient Processing: Binary operations are faster and use less power.

    How Binary Numbers Work (With Examples)

    Binary Number System Operates by using Positional Notation. Binary and Decimal follow the same basic principles. Binary uses powers of 2 where decimal uses powers of 10. To understand how binary numbers work, let’s understand Positional Notation. 

    Introduction to Positional Notation System

    A way of writing numbers in a position where the position of each digit determines its value is called a Positional notation. 

    In positional notation, each digit in a number is multiplied by a value based on its position. The place value increases by powers of the base. 

    For example

    We’ll break it down by position (from right to left), using powers of 2:

    Position (from right)3210
    Binary Digit1010
    Power of 22³2²2¹2⁰
    Value8020

    Binary to Decimal Conversion (Step-by-Step)

    After you understand the Positional Notation, converting Binary to decimal will be way easier. You just need to multiply each binary digit by 2 to the power of its position starting from right. Lastly, add them up. 

    As we did in the above table, let’s convert the same value 1010 to decimal.

    Position (from right)3210
    Binary Digit1010
    Power of 22³2²2¹2⁰
    Value8020

    Step-by-Step Calculation:

    1. 1 × 2³ = 8
    2. 0 × 2² = 0
    3. 1 × 2¹ = 2
    4. 0 × 2⁰ = 0

    Now add the values:
     8 + 0 + 2 + 0 = 10

    Finally 

    Binary 1010 = Decimal 10 

    How to use a Binary Calculator 

    A binary calculator is a very user-friendly tool that’ll save a lot of time by quickly performing arithmetic operations using binary numbers. It’s useful for everyone whether you are a student, developer, or just curious about binary. 

    On our site, we’ve offered 3 different calculators focusing on Binary. They are:

    1. Binary Calculator
    2. Binary to Decimal Calculator
    3. Decimal to Binary Calculator


    Let’s see it’s uses one-by-one:

    1. Binary Calculator

     For Arithmetic Operations (Add, Subtract, Multiply, Divide)

    Steps:

    1. Input the first binary number
    2. Select the operation symbol (+, –, ×, or ÷)
    3. Input the second binary number
    4. Click Calculate
    5. View the binary and decimal result

    2. Binary to Decimal Calculator

    Convert Binary Numbers into Decimal

    Steps:

    1. Input the binary number
    2. Click Calculate
    3. View the decimal result

    3. Decimal to Binary Calculator

     Convert Base-10 Numbers into Binary

    Steps:

    1. Input the decimal number
    2. Click Calculate
    3. View the binary result

    Summary Table

    CalculatorFunctionBest For
    Binary CalculatorAdd, subtract, multiply, divide in binaryMath operations
    Binary to Decimal CalculatorConvert binary to base-10Understanding binary values
    Decimal to Binary CalculatorConvert base-10 to binaryBinary encoding and conversions

    When to use a binary calculator 

    You should use a binary calculator when:

    • You’re dealing with long binary numbers
    • You need to perform binary arithmetic operations quickly
    • You’re double-checking manual conversions
    • You’re learning and want instant feedback

    Binary Code Applications in Real Life

    Binary code isn’t limited only in textbooks, it has played a lot of role in the tools around you. From smartphones you use after each minute to satellites, binary is widely used in the digital world. It is the language that machines understand.

    Some areas where Binary code is used are:

    1. Computers and CPU Operations

    • Every command a computer executes is translated into binary instructions for the CPU.
    • Programs, files, images, and videos are all stored as binary data.
    • Even high-level programming languages are ultimately compiled into binary.

    Example: When you press a key, the keyboard sends a binary signal to the computer’s processor to interpret it.

    2. Digital Electronics

    • Devices like smartphones, smart TVs, digital watches, and calculators work using binary logic gates.
    • These gates control how electrical signals flow — based on whether they’re ON (1) or OFF (0).

    Example: A calculator adds two numbers by converting them to binary, processing them, and converting the result back to decimal.

    3. Cryptography & Secure Communication

    • Modern encryption methods use binary data to encode, transmit, and decode messages.
    • Data is encrypted into binary sequences to protect it during transmission (e.g., over Wi-Fi or in messaging apps).

    Example: WhatsApp uses binary encryption behind the scenes to keep your messages private.

    4. Artificial Intelligence & Machine Learning

    • Binary data is at the core of training models — inputs, outputs, and decisions are encoded in binary form.
    • Neural networks and decision trees often rely on binary classification (yes/no, 1/0).

    Example: AI deciding whether an email is spam or not can be based on binary outcomes.

    5. File Formats & Storage

    • Files like images, videos, and documents are saved in binary formats (e.g., .jpg, .mp4, .pdf).
    • Hard drives, SSDs, and memory chips store and read data as sequences of bits.

    Example: A single photo on your phone is just a long line of 0s and 1s that your device renders into pixels.

    6. Gaming, Audio & Video

    • Binary is used to store sound frequencies, video frames, player input, and game logic.
    • Game consoles and PCs convert binary game code into interactive experiences.

    Example: Pressing “jump” in a game sends a binary input to trigger animation.

    Binary Files: What Are They and How Do They Work?

    After saving the file or after downloading, you’ll find it in either text file or a binary file. So, let’s understand what a binary file is:

    A binary file is a type of file which stores data in a binary format (0 and 1). The files aren’t meant to be read by humans. It can contain anything like images, video, audio, software programs, or even compressed data.

    In the context of text files, the stored data can be easily read by humans. But, the data stored in the Binary file has to be processed by the computer.

    “.exe, .jpg, .mp3, .pdf, .zip, .mp4” are the types of Binary files.

    How Do Binary Files Work?

    1. The file stores raw binary data (0s and 1s)
    2. A program (like VLC, Word, or Photoshop) reads and interprets the data
    3. You interact with it in a meaningful way — like viewing a video or editing a photo

    Example: When you open a .jpg image, your computer reads the binary data and renders it as a picture.

     Are Binary Files Executable?

    Some binary files can be executable, meaning they tell the computer to perform specific tasks. These are program files like:

    • .exe (Windows apps)
    • .bin (firmware or boot files)
    • .dll (Dynamic Link Libraries)

    Opening unknown binary executable files can be risky — they might contain malware.

    Frequently Asked Questions (FAQs)

    What is binary in real life?

    In real life, binary refers to anything that works in two states, like on/off, true/false, or 0/1. Most digital devices including computers, smartphones, and smartwatches use binary code to process and store data. 

    For example, your phone camera stores each pixel as a series of 0s and 1s. Binary logic is also used in automation, AI, and embedded systems found in modern electronics.

    What is binary explained easily?

    Binary is a way of counting and storing information using only two numbers: 0 and 1. Each binary digit (called a bit) represents a small part of data. Computers read these 0s and 1s as electrical signals—off for 0, on for 1. When combined, bits can represent text, images, audio, and software instructions.

    What is the easiest way to calculate binary?

    The easiest way to calculate binary is using the positional value method with powers of 2. Start from the rightmost digit, assign each digit a power of 2 (1, 2, 4, 8, etc.), multiply each bit by its value, then add the results to get the decimal. For quick conversions, use a binary to decimal calculator.

    Example: 1010 → (1×8) + (0×4) + (1×2) + (0×1) = 10

    How does binary analysis work?

    Binary analysis is the process of examining raw binary code (0s and 1s) to understand how files, software, or systems behave. It’s commonly used in cybersecurity, malware reverse engineering, and digital forensics to decode compiled files or inspect executables. Analysts study binary patterns to trace logic, detect vulnerabilities, or recover data.

    What is binary all about?

    Binary is the core of modern computing. It’s a base-2 number system made up of only two digits: 0 and 1. Every file, program, and digital interaction—from browsing websites to playing games—is made possible by binary code. It’s how computers represent, store, and process information efficiently.