Suppose, you are calculating the Weight of rice you produced this year. It weighed 10000000000 kg. So, while noting, writing 109 Kg will be easier than writing 10000000000 kg. So here, 9 is the exponent of 10. Which means, 10 is multiplied 9 times by itself. It can be broken down as 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 = 109 . This example is read as 9 is the power of 10 or 10 to the power 9.
The process of expressing large numbers in terms of power is called exponents. The exponent of a number indicates the total times to use that number in a multiplication. 7×7×7 can be expressed as 73 because 7 is multiplied 3 times by itself which results in 343. The 3 in this example is called ‘exponents’ or ‘power’ which tells how many times 7 can be multiplied.
Let’s take few more examples:
82 = 8×8 = 64
(Here, 2 is the exponent which tells 8 can be multiplied 2 times.)
63 = 6×6×6 = 216
(Here, The exponent 3 tells that 6 should be multiplied 3 times.)
But, there are some exceptional cases. Such as:
4 0 = 1
(We must keep in mind that when the exponent is 0, the result will be 1.)
Exponents are commonly used in:
- Scientific notation (e.g., 6.02 x 1023 )
- Algebra and calculus
- Computer science and data analysis
- Real-world applications like compound interest and population growth
Exponents in Math: Definition & Basics
Exponents has a simple definition, it tells you how many times to multiply the base by itself.
Terms to understand:
- Base: The number being multiplied.
- Exponent (or power): Tells how many times the base is used as factor.
Example: 53 = 5 x 5 x 5 = 125
This is read as “Five raised to the power of three” or “Five Cube”
Why Are Exponents Important in Math?
Exponents help express very large or very small numbers in a compact form. They’re essential for:
- Simplifying calculations
- Expressing patterns and repeated multiplication
- Calculating growth in finance and science
- Programming and algorithms
Basic Exponent Rules (With Examples)
There are some laws of exponents in mathematics.
Product Rule
am x an = am+n
Example:
23 x 24 = 23+4 = 27 = 128
Quotient rule
$$\frac{a^m}{a^n} = a^{m-n}$$ (when a ≠ 0) Example: $$\frac{5^5}{5^2} = 5^{5-2} = 5^3 = 125$$
Zero Exponent Rule
$$a^0 = 1$$ (when a ≠ 0) Example: $$7^0=1$$
Negative Exponent Rule
$$a^{-n} = \frac{1}{a^n}$$ Example: $$3^{-2} = \frac{1}{3^2} = \frac{1}{9}$$
Power of a Power Rule
$$(a^m)^n = a^{m \cdot n}$$ Example: $$(2^3)^2=2^(3 \cdot2)=2^6=64$$
Power of a Product Rule
$$(ab)^n = a^n \cdot b^n$$ Example: $$(2 \cdot 3)^2 = 2^2 \cdot 3^2 = 4 \cdot 9 = 36$$
Power of a Quotient Rule
$$\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}$$ Example: $$\left(\frac{4}{2}\right)^2 = \frac{4^2}{2^2} = \frac{16}{4} = 4$$
Fractional Exponents
$$a^{\frac{m}{n}} = \sqrt[n]{a^m}$$
Example:
$$8^{\frac{1}{3}} = \sqrt[3]{8} = 2$$
Common Mistakes with Exponents
There are some common mistakes that exponents learners make:
- Confusing base vs. exponent: 23 ≠ 32
- Adding exponents when bases differ: 22 + 32 ≠ 54
- Wrong sign handling in negative exponents: -22 ≠ (-2)2
Exponent Calculator (Interactive Tool)
Use this calculator to compute any exponent quickly:
- Enter base and exponent
- Click Calculate
- Get instant result with simplified expression
How to Use the Exponent Calculator:
- Input a base number (e.g., 5)
- Input exponent (e.g., 3)
- Click “Calculate”
- Output:
Try it for fractional or negative exponents too!
Advanced Topics: Exponents with Variables & Logs
Exponents with Variables
$$x^a \cdot x^b = x^{a+b}$$ Often used in algebraic expressions.
Derivatives of Exponential Expressions
In calculus, the derivative of $$a^x$$ is: $$\frac{d}{dx} \left( a^x \right) = a^x \ln(a)$$
Logarithms and Exponents
$$[
\log_b \left( a^c \right) = c \cdot \log_b(a)
]$$
Logs are the inverse of exponentiation.
Exponents are powerful tools in both basic and advanced mathematics. By understanding their rules—like the product, quotient, and power laws—you can simplify complex expressions, solve problems faster, and grasp algebra and calculus concepts with ease.
Don’t forget to use the Exponent Calculator above for quick and accurate solutions to any exponent-related math problem.
FAQs on Exponents
1. What is an exponent in math?
An exponent shows how many times a number is multiplied by itself.
2. What are the rules of exponents?
They include product, quotient, zero, negative, power, and fractional rules.
3. How do you multiply exponents?
Add exponents if bases are same: $$a^m \cdot a^n = a^{m+n}$$
4. What does a negative exponent mean?
It means reciprocal: $$a^{-n} = \frac{1}{a^n}$$
5. Can exponents be fractions?
Yes. $$a^{\frac{1}{2}} = \sqrt{a}$$ , etc.
6. How to type an exponent?
Use superscript in Word or ^ symbol (e.g., 2^3).
7. What is the zero exponent rule?
Any non-zero number to the power of 0 equals 1.
8. What’s the difference between exponents and powers?
They are often used interchangeably, but “power” can refer to the whole expression an.
9. How to simplify exponents?
Use exponent laws to combine and reduce expressions.
10. Is there a calculator for exponents?
Yes, use the tool above or a scientific calculator.
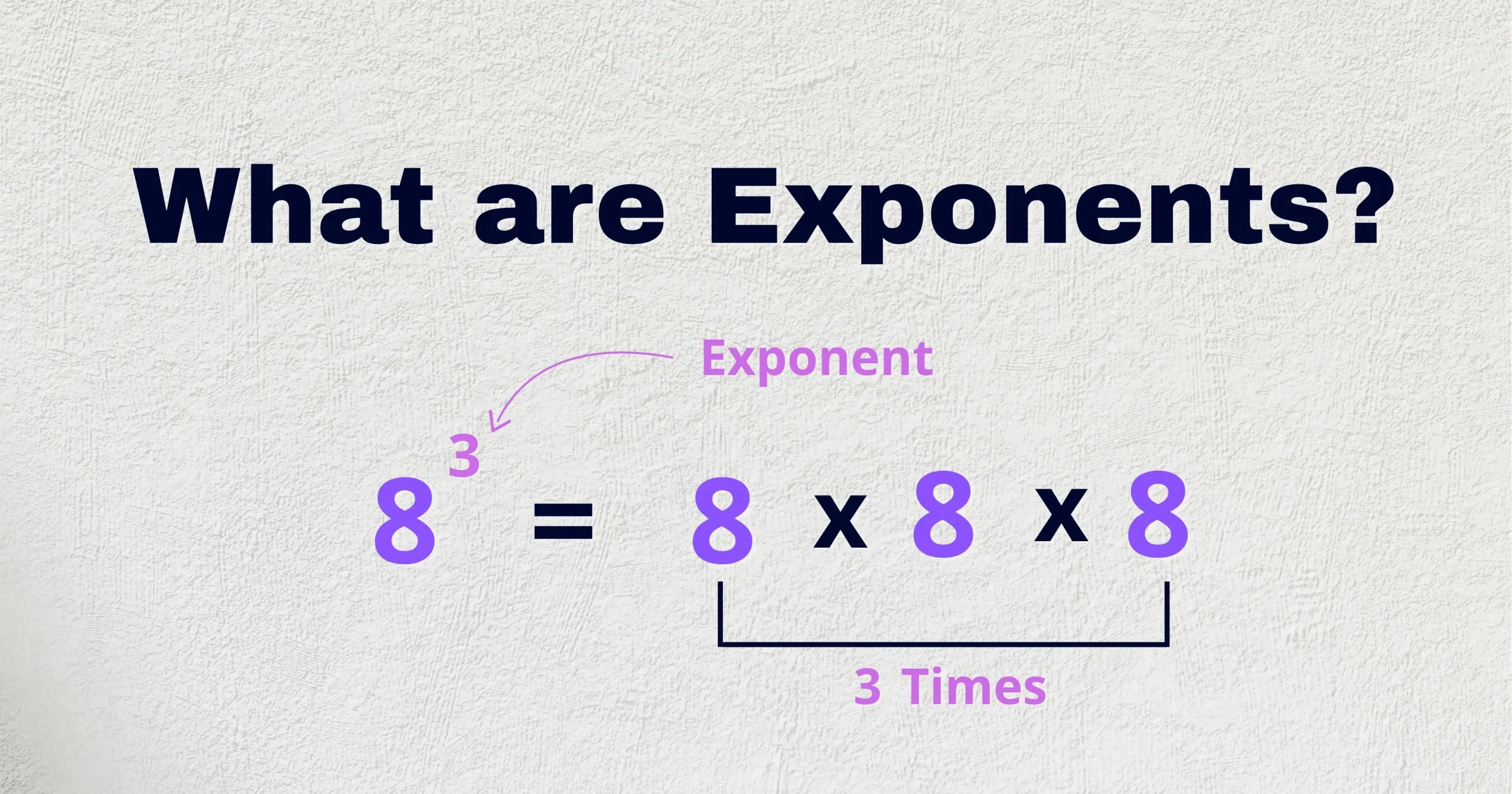
Leave a Reply